mat2 egzamin pytania 1termin sesja lato 08

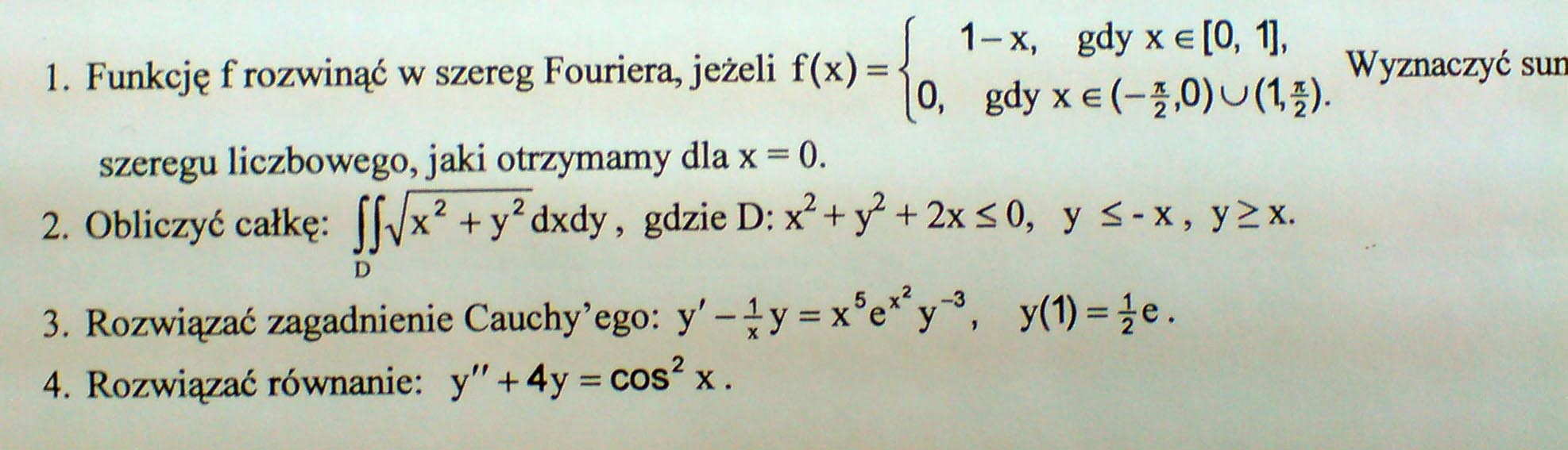
1 - x, gdy x e [0,1], gdyxe(-f,0)u(1,f).

Wyznaczyć

1. Funkcję f rozwinąć w szereg Fouriera, jeżeli f(x) =

szeregu liczbowego, jaki otrzymamy dla x = 0.

2.    Obliczyć całkę: JJ^x² +y²dxdy, gdzieD: X²+y² + 2x£0, y £-x, y>x.

D

3.    Rozwiązać zagadnienie Cauchy’ego: y'-4y = x⁸e^x y^-3, y(1) = ^e.

4.    Rozwiązać równanie: y" + 4y = cos² x.