S5008123

44

44

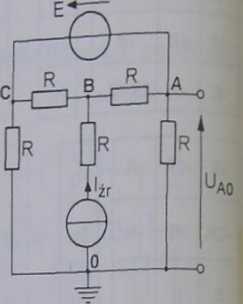
Rys. 1.34a

usunąć ze schematu połączony

Dane: E = 24V, 1^= 12A, R = 2(ł.

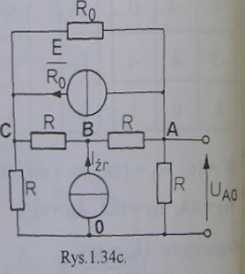
Rozwiązanie: Ponieważ obwód zawiera idealną siłę elektromotoryczną to w szereg z nią zostanie wprowadzony dodatkowy rezystor Ro (który w rzeczywistości równy jest zeru Go -> a>) i dopiero po uzyskaniu wyrażenia na Uo obliczona zostanie jego granica przy Go->“. Rysunki 1.34b i c pokazują drogę kolejnych przekształceń. Ponieważ źródło prądowe jest źródłem idealnym to jego rezystancja wewnętrzna

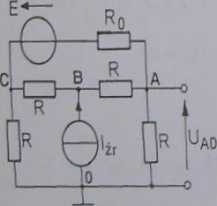
Rys.l.34b

jest równa nieskończoności, można w szereg ze źródłem prądu rezystor R.

Oznaczenia:

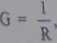
V_a=Vao.

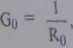
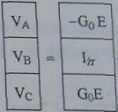
Va, V_B, Vc - potęcjały węzłów A, B, C

Układ równań dla metody potencjałów węzłowych opisujący schemat z rysunku 040.

G₀ _Q 2G+Gq

2G+Go -Go -Go

-G 2G -G

Po obliczeniu wyznacznika głownio otrzymuje się:

W = 4G²G₀ + 4G³, a po obliczeniu wyznacznika W a

W_a=-2G²GoE + 2GGoIżt ⁺ 2G²I_Ji .

Dla potencjału Va ważne jest następujące wyrażenie

-2G²GqE + 2GGpIj_r+2G²I_żr ^A” 4G²G₀+4G³

a po podzieleniu przez Go i policzeniu granicy wyrażenia dla Go -* °o

Po wstawieniu danych Uao 3 0.

Odpowiedz: Napięcie Uao ⁼ 0V.

Zadanie 1.45

W obwodzie z rysunku 1.33a obliczyć prądy gałęziowe stosując metodę potencjałów węzłowych. Dane identyczne jak w zadaniu 1.42. Prądy będące do obliczenia naniesiono na schemacie przedstawionym na rysunku 1.33c.

Odpowiedź: Iio=8A, l2o=I2A, I₃o=-4A, Ii2 = 0A, I23 = »2A i bi=8A. Zadanie 1.46

Obliczyć napięcie U_Ao z zadania 1.44 stosując metodę prądów Oczkowych.