scan(

' y² = 12* - xy I -2y - y + * = 14 - 24 ' f = 14 - jc

U = 12-y

' y² = 12* - xy I -3y + * = -10 ' f = 14 - * _k ^z = 12 - y

' y² = 12* - *y

_y² = 12 (3y -10) — (3y — 10)y    w miejsce * podstawiamy 3y-10

*    = 3y -10 ' r = 14 — * l z = 12 - y

y² = 36y -120 - 3y² + lOy    to równanie trzeba uporządkować

*    = 3y - 10 ⁴ f = 14 - *

. z = 12 - y

” y² - 36y +120 + 3y² - lOy = 0

*    = 3y - 10 ' r = 14 - *

. z = 12 - y

*    = 3y - 10

I r = 14 — *    rozwiązujemy równanie kwadra-

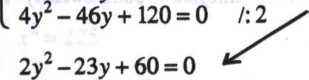
z = 12 - v    towe posługując się wzorami

A = b² - 4ac

lub

A = (23)² - 2 • 4 • 60 = = 529 - 480 = 49

VA = 7

_-(-23)-7 _ 23-7 _16 ^

^>l 2 2    4    4

_v _ -(-23)+7 _ 23 + 7 _30 __7S ^>2~    2 2    "4    ~ 4    ’

Znalezione wartości y podstawiamy do równań:

najpierw = 4

x = 3- 4-10=12-10 = 2 t = 14 - * = 14 - 2 = 12

	z	= 12	II 1 <N t-H II JK 1	8
czyli
	x = 2,y =	4, z	= 8, t = 12
teraz	y2 = 7,5
	X	= 3y	- 10 = 3-7,5-	10 =
	t	= 14	-* = 14-12,5	= 1,5
	z	= 12	- y = 12 - 7,5 =	= 4,5
czyli
	x = 12,5;	y-'	7,5; z = 4,5; t =	1,5
Odp.	r x = 2		[x = 12,5
	y = 4 lub		y= 7,5
4	z = 8	i	z = 4,5
	f = 12		r = 1,5

Zad.13.

Wyznacz liczbę dodatnią jc taką, aby ciąg 5, x, 45 był ciągiem geometrycznym.

Rozwiązanie:

5, x, 45 jest geometryczny, gdy iloraz dowolnego wyrazu i wyrazu bezpośrednio go poprzedzającego jest stały (jest liczbą)

59