Sieci CP str051
51
Rozdział 4. Nieliniowe nieci neuronowe
<p(e) -, 1
e
Taka postać ma sporo wad, od niej jednak zaczniemy dyskusję, gdyż przy tej postaci funkcji najłatwiej jest wprowadzić pewne intuicje przydatne potem przy dyskusji wszelkich nieliniowych sieci neuronowych. Zacznijmy od odnotowania najbardziej naturalnego faktu: ponieważ sygnał wyjściowy perceptronu przyjmuje dyskretne wartości (y = Huby = 0), przeto może być rozważany w kategoriach określonej decyzji (na przykład — obiekt należy do rozpoznawanej klasy lub obiekt, do niej nie należy). Możliwa jest także interpretacja oparta na logice matematycznej — sygnał y = 1 można wówczas interpretować jako ,.prawda”, a sygnał y = 0 jako ,,fałsz”. Przy pierwszej interpretacji perceptron może być traktowany jako układ dokonujący pewnego podziału wejściowego zbioru sygnałów X na dwie klasy: klasę wyróżnioną (dla której y = 1) oraz klasę odrzuconą. Przy drugiej interpretacji perceptron może być rozpatrywany jako układ realizujący pewną funkcję logiczną, a więc automat skończony. Druga interpretacja jest wcześniejsza, w istocie pierwsze prace dotyczące sieci neuronowych Me.Culloe.lia i PIttsn [McCu43] taką właśnie proponowały interpretację, a rozwijana na gruncie logiki matematycznej teoria funkcji progowych stanowi dla tego podejścia wygodny fundament matematyczny. Obszerniejsze informacje na ten temat zawarto w książce [TadeOla].
4.2 Właściwości nieliniowego modelu neuronu
Z dyskretnymi wartościami sygnału wyjściowego z nieliniowego modelu neuronu wiąże się następujące zagadnienie. Zależnie od postaci przyjętej funkcji yj(e) sygnał i/ można rozpatrywać jako binarny y € {0,1} lub bipolarny y € {-1,1). Na pozór jest to różnica mało istotna, gdyż za pomocą trywialnego przeskalowania można oczywiście swobodnie przejść od jednej postaci sygnału do drugiej. Jednak w rzeczywistości różnica może być dość istotna, ponieważ punkty należące do zbioru {0,1} są wierzchołkami jednostkowego hi per.sześcian u w 7vn, natomiast punkty należące do zbioru {-1, 1} leżą na powierzchni jednostkowej sfery w 7vn. Intuicja wywodząca się z dwu- i trójwymiarowej przestrzeni podpowiada, że sfora jest podobna do sześcianu, oto sfera może być porównana z sześcianem o zaokrąglonych wierzchołkach. Tymczasem w o-wymiarowej przestrzeni sfera i sześcian różnią się w sposób zasadniczy, o czym można się przekonać porównując na przykład objętość kuli o promieniu r z objętością sześcianu o boku l. Objętość sześcianu wynosi oczywiście Vs — ł". natomiast objętość kuli wyraża się bardziej skomplikowaną formula:
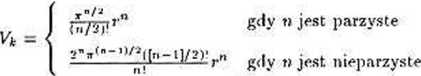
Wyszukiwarka
Podobne podstrony:
img051 51 Rozdział 4. Nieliniowe nieci neuronowe<p(e) i, 1e Taka postać ma sporo wad, od niej jed
Sieci CP str039 39 Rozdział 3. Liniowe siwi neuronowe mu taką strategię uczenia, by zapamięta] i pot
Sieci CP str057 57 Rozdzia.1 4. Nieliniowe sieci neuronowe — funkję BSB (Rrain State in a Uoz): 1 gd
Sieci CP str059 59 Rozdział 4, Nieliniowe sieci neuronowe4.6 Uczenie sieci nieliniowej Opinany wyżej
Sieci CP str057 57 Rozdzia.1 4. Nieliniowe sieci neuronowe — funkję BSB (Rrain State in a Uoz): 1 gd
Sieci CP str061 61 Rozdział 4. Nieliniowe sieci neuronowe Na samym początku wyznacza się zatem popra
Sieci CP str063 63 Rozdział 4. Nieliniowe sieci neuronowe klasycznej metody backpropagalion z wykorz
Sieci CP str037 37 Rozdział 3. Liniowe sieci neuronowe pokazano jedynie oczy i usta). Takie zadanie
więcej podobnych podstron