skanowanie0075

^a2 — ^e3^r> Gi? = s₂ • 2 r,    g₃ • 2 r = s₂r

M„_edB = 2M—2mgr (/icosa + sina)—0,5mgf

T 1    ⁸⁷    2

hredB = -rr-mr*

O

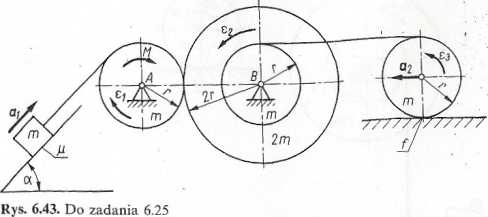
Zadanie 6.26. Układ składający się z czterech kół i dwóch ciał pokazano na rys. 6.44. Przez koło o masie m kg i promieniu r m, zamocowano przegubowo w punkcie A, przerzucono linę, na której końcu zawieszono ciało o masie 2m. Drugi koniec tej liny zaczepiono w środku B dwóch współśrodkowo zamocowanych kół o masach m i 3m oraz promieniach r i 3r. Koła te toczą się bez poślizgu po poziomym torze, gdzie współczynnik tarcia tocznego wynosi f Na obwodzie dużego koła nawinięto drugą linę, którą przerzucono przez krążek o masie m i promieniu r, zamocowany przegubowo w punkcie C. Na końcu tej liny przywiązano ciało o masie m, leżące na równi pochyłej o kącie pochylenia a. Wyznaczyć przyspieszenia kątowe i liniowe poszczególnych elementów układu oraz moment M_zredA i moment bezwładności l_zreiA. W chwili początkowej układ znajdował się w spoczynku.

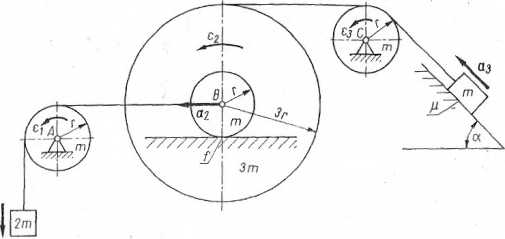
Rys. 6.44. Do zadania 6.26

Odpowiedź

2 mgr

fii =-

1—2( -^-t-sina+jucosa

ai = fi,r

43,5mr²

^a2 ~ ^ei^r> ^a2 ⁼ ®2^r> e₂ ‘ 4r = s₃r, a₃ = e₃r

1—2( —I- sina+/icosa

> hredA = 43,5mr²

Zadanie 6.27. Układ przedstawiony na rys. 6.45 leży w płaszczyźnie pionowej. Masa pręta O A = 3r wynosi m kg. Masa koła ruchomego o promieniu r m jest równa m kg. Promień koła nieruchomego, po którym toczy się bez poślizgu koło ruchome, wynosi 2r m. Koło ruchome toczy się również bez poślizgu po obręczy o masie m i promieniu 4r. W chwili początkowej układ pozostawał w spoczynku i pręt O A zajmował położenie poziome. Obliczyć przyspieszenia kątowe poszczególnych elementów układu po jego obrocie o kąt <p_v

Rys. 6.45. Do zadania 6.27

Odpowiedź

e₂ = 3e_lf e₃ = l,5e_l

2 M + 9mgr (1 — cos q>) ^{Sl =}    2-52,5 mr²

Zadanie 6.28. Układ pokazany na rys. 6.46 składa się z czterech współpracujących ciernie tarcz kołowych. Do tarczy o promieniu r_t m i masie m_i kg przyłożono stały moment M_x N-m, który napędza cały mechanizm. Moment hamujący M₃ N-m przyłożono do tarczy o masie ml kg i promieniu r₃ m. Wyznaczyć przyspieszenia kątowe poszczególnych tarcz, moment układu M_zred0 i moment bezwładności zredukowany do osi O_x - I_zred0l. W chwili początkowej układ znajdował się w spoczynku.

173