Scan0001 (3)

LABORATORIUM Z KRYSTALOGRAFII

Temat ćwiczenia: Wyznaczenie zawartości komórki elementarnej kryształu w oparciu o pomiar gęstości kryształu

Wprowadzenie

1, Zawartość komórki elementarnej Zkf

Ważnym etapem rentgenowskiej analizy strukturalnej kryształów jest wyznaczenie zawartości komórki elementarnej (KE) => Zke, czyli liczby cząsteczek w komórce elementarnej. Cząsteczką stechiometryczną (formalną) nazywa się zbiór atomów odpowiadający wzorowi chemicznemu danej substancji. Liczba cząsteczek przypadająca na komórkę elementarną pozostaje w związku z symetrią translacyjną kryształu opisaną przez grupę przestrzenną.

Liczbę Zke wyznacza się na podstawie znajomości dwóch wielkości fizycznych:

1)    wymiarów komórki elementarnej (objętości komórki Vke )

2)    gęstości komórki elementarnej

i

ad 1)

W metodach rentgenowskiej analizy strukturalnej poszukiwanie wymiarów KE opiera się na analizie kierunków ugiętych promieni dyfrakcyjnych.

Kształt i wymiary KE określone są przez sześć parametrów zwanych stałymi sieciowymi

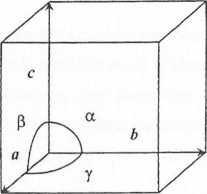
są to długości krawędzi komórki: a ,b ,c określane w angstremach [A] (lA=10'¹⁰m),

oraz kąty między osiami krystalograficznymi: a, (5, y określane w stopniach [°],

1

Instrukcja opracowana przez Agnieszkę Rybarczyk-Pirek, 2011

Objętość komórki elementarnej jest iloczynem mieszanym trzech wektorów:

V_ke=5«(6xc);    (bxc) = bcsina    (1)

Znajomość sześciu stałych sieciowych pozwala obliczyć Vke na podstawie wzoru:

Yjrg = abc-yfl - cos²a - cos² fi - cos²y + 2cosa cosfi cosy    (2)

ad 2)

Teoretycznie gęstość pojedynczej KE powinna być taka sama jak gęstość całego kryształu (skończony zbiór wszystkich KE). Matematyczne zależności między tymi wielkościami podają poniższe równania.

Gęstość (masa właściwa) wyraża się wzorem: p = m / V [g/cm³]    (3)

W przypadku pojedynczej KE: pke ⁼ eike/ V_Ke [g/A³]    (4)

gdzie mKE oznacza masę komórki elementarnej, czyli sumaryczną masę wszystkich atomów w komórce wyrażoną w gramach (rzeczywistym obiektem znajdującym się „wewnątrz” abstrakcyjnej komórki elementarnej są atomy). Jeśli weźmiemy pod uwagę masę pojedynczej cząsteczki wyrażoną w gramach, to masa komórki elementarnej będzie iloczynem masy cząsteczki i liczby cząsteczek w komórce

mj(£ Zke ^p ^cząsteczki    (^)

Najczęściej operujemy nie masą cząsteczki wyrażoną w gramach, lecz masą molową, którą łatwo obliczyć na podstawie znajomości wzoru sumarycznego związku. Wówczas masę cząsteczki w gramach otrzymuje się z ilorazu masy molowej M i liczby Avogadro N i (N=6.023 10²³):

^cząsteczki / N    (ń)

gdzie M - masa molowa danej substancji, N - liczba Avogadro. Wstawiając(5) i (6) do wzoru (4) otrzymuje się następującą zależność:

Pke = (Zke-M)/(N-VKE) = [g/A³]    ~p_m

Instrukcja opracowana przez Agnieszkę Rybarczyk-Pirek, 2011