skanuj0012

52

i kondensatora

2 _ 1

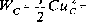
— C|{/_mC|²c°s²(⁽ot + Q') .

(2.102)

Wartości maksymalne tych energii

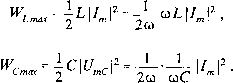
(2.103)

(2.104)

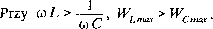
Na rys. 2.15a naniesiono również moc chwilowa całego fragmefllu reaktancyjnego LC P_x = u_xi = {u_L + u_c)i =p_L*p_c = (\U_L\ - |I/_c|)|/|sin(2wr+ 2a) .

Na podstawie wykresu promieniowego z rys. 2.14

\^UmL\-\V_mC\ = i^unu\ ⁼ I^Jsintp, więc \U_L\-\U_C\ = |I/|sin<p ,

czyli

(2.105)

p_x = |ł7| |/|sin(psm(2o>t + 2a) .

Amplituda mocy p_x wynosi 11/| |/| sin^. Moc p_x nie ma składowej stałej, więc moc czynna fragmentu reaktancyjnego jest zerowa

T

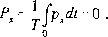
Na podstawie mocy chwilowych całego układu i fragmentu reaktancyjnego wprowadza się definicje pozostałych mocy. Wprowadzone poprzednio moc chwilowa i moc czynna zostaną tu też zestawione. Moce p i p_x przedstawione są na rys. 2.16.

Moc chwilowa dla dowolnych przebiegów jest to iloczyn chwilowych wartości napięcia i prądu

(2.106)

(2.107)

df

P = u i,

a dla przebiegów sinusoidalnych

P - \U\ |f|cos<p - \U\ |/|cos(2co< + 2o: + (p) .

Jednostką mocy chwilowej jest 1 VA.

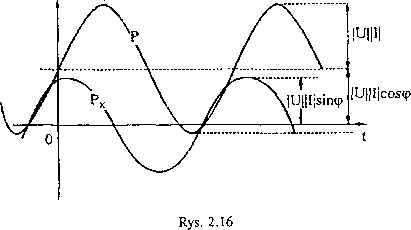
Moc czynna (dla przebiegów okresowych) jest to wartość średnia za okres z mocy chwilowej

_VT

ptlfpdt,    (2-108)

a dla przebiegów sinusoidalnych

P = \U\ 1 /1costp .    (2-109)

Jednostka mocy czynnej jest 1 W (wymiarowo: V-A).

Moc pozorna jest zdefiniowana dla przebiegów sinusoidalnych jako amplituda składowej zmiennej mocy chwilowej całego układu

\S\=\U\\I\.    (2-HO)

Jest to moc, która określa wielkość źródła.

Jednostka mocy pozornej jest 1 V-A. Dla dowolnych przebiegów okresowych niesinusoidalnych (zwanych odkształconymi) również definiuje się moc, która jest iloczynem skutecznych wartości napięcia i prądu całego układu. Nosi ona wtedy nazwę mocy pozornej lub modułowej.

Moc bierna dla przebiegów sinusoidalnych jest zdefiniowana jako amplituda mocy chwilowej w elementach biernych.

2= |ŁJ||/|sin<p.    (2-Hl)

Ponieważ -90’ < ę < 90", więc moc bierna może być dodatnia dla tp >0 (moc bierna indukcyjna), lub ujemna dla tp < 0 (moc bierna pojemnościowa). Jednostką mocy biernej jest 1 var (od pierwotnej jednostki V-A_r - wolt amper reaktywny).