skanuj0013

liy obliczyć niepewność maksymalną (Ąy)_max wystarczy pomnożyć obliczoną wartość y przez niepewność względną (18).

6. Opracowanie wyników pomiaru wielkości zależnych

Do opracowania wyników pomiarów dwóch wielkości zależnych x oraz y mjczęściej stosujemy metodę graficzną.

\>niżej podajemy zasady odręcznego wykreślania zależności funkcyjnych:

1.    Wykresy wykonujemy na papierze milimetrowym.

2.    Na osiach układu zaznaczamy wielkości odkładane oraz ich jednostki.

3.    Wybieramy skalę tak, by:

a)    niepewności pomiarowe nie przekraczały 5 mm,

b)    łatwo dało się odczytać współrzędne punktów,

c)    nachylenie krzywej (w przypadku szczególnym nachylenie prostej) w najbardziej interesującym nas obszarze było bliskie 45°,

d)    na osi znajdował się cały przedział zmienności wielkości fizycznej z niewielkim nadmiarem, co oznacza, że podziałka nie musi się zaczynać od zera.

4.    Punkty pomiarowe wyraźnie zaznaczamy: krzyżykami, iksami (wtedy punkt pomiarowy znajduje się w miejscu przecięcia), kółkami, trójkątami, kwadratami (punkt pomiarowy jest w środku figury).

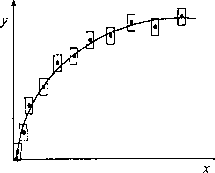
Rys.5. Przykładowa krzywa doświadczalna z zaznaczonymi prostokątami niepewności

5.    Nanosimy niepewności pomiarowe dla wszystkich lub prawie wszystkich punktów. Niepewności wyznaczają wokół punktów pomiarowych prostokąty niepewności. Bokami tych prostokątów są podwojone wartości niepewności, a w ich środku geometrycznym znajdują się punkty pomiarowe.

6.    Wykreślamy krzywą (prostą) prowadząc ją tak między punktami pomiarowymi, by przechodziła przez wszystkie prostokąty niepewności maksymalnych lub około 70% prostokątów niepewności określonych przez odchylenia standardowe (rys.5). Punkty pomiarowe powinny być rozmieszczone równomiernie po obu stronach krzywej (prostej). Proste rysujemy za pomocą linijki, natomiast przy zależnościach nieliniowych posługujemy się krzywikiem. Nie łączymy punktów pomiarowych łamaną!

W praktyce najczęściej korzystamy z dostępnego w laboratorium programu komputerowego WykresLab, który dopasowuje krzywą do otrzymanych wyników pomiarów i oblicza odpowiednią niepewność dopasowania.

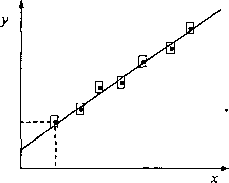
Rys.6. Punkty pomiarowe wraz z zaznaczonymi niepewnościami

6.1. Opracowanie wyników pomiaru wielkości zależnych liniowo

Załóżmy, że mierzone wielkości fizyczne x i y związane są zależnością liniową:

y = ax + b. (19)

Współczynniki a i b na ogół mają interpretację fizyczną. Na przykład dla zależności drogi od czasu w ruchu jednostajnym współczynnik kierunkowy jest równy prędkości (s ’= v-f), w zależności napięcia od natężenia prądu współczynnik kierunkowy jest równy oporowi {U = RI). Określając z wykresu parametry a i b prostej możemy więc wyznaczyć niektóre wielkości fizyczne.

Aby obliczyć współczynniki a i b prostej (19) posługujemy się metodą regresji liniowej, na której oparty jest program WykresLab dopasowujący wykres prostej do punktów pomiarowych oraz wyliczający dla niej współczynniki regresji liniowej a i b.

Wyniki pomiarów składają się z n par liczb z,, y,- oraz ich niepewności pomiarowych At,-, Ay,- (rys.6). Gdy są to niepewności systematyczne, a tak jest najczęściej, stosujemy klasyczną regresję liniową. Średnie wartości współczynników a i b dobieramy tak, by spełniały postulat Gaussa, to znaczy, by suma kwadratów odchyleń:

i=i    ;=i