skanuj0024

46

jąc wzór (1) będzie rzędu 0,1%, co daje błąd bezwzględny Ag rzędu 0,01 m/s². Jeśli niepewność wyznaczenia g będzie rzędu 1% lub większa, to błędy systematyczne, o których była tu mowa możemy zaniedbać, w przeciwnym razie powinniśmy użyć dokładniejszego wzoru np.:

4tc²/ L 1 . ₂(<p_m g = —l + -sin — ^S T² \    4 I 2

lub

g = -

4tc²/

101 /

1 + — sin² f— 4    2

jeśli wpływ czynnika ~fy

nie jest do zaniedbania.

Na zakończenie analizy błędów systematycznych towarzyszącej naszej metodzie pomiarowej zwróćmy jeszcze uwagę na występującą we wzorze (4) liczbę 7t. Jak wiadomo stosowanie przybliżonych wartości stałych fizycznych lub matematycznych jest również źródłem błędów systematycznych. Zastanówmy się z jaką najmniejszą dokładnością należy wprowadzić do wzoru (4) liczbę tc, żeby wpływ tego przybliżenia na wyznaczenie g był nie większy niż czynników fizycznych, które rozważaliśmy. Załóżmy, że satysfakcjonuje nas błąd procentowy rzędu 0,01%, wówczas spełniona musi być nierówność:

--100 <0,01%,

71

gdzie An jest różnicą między wartością dokładną a naszym przybliżeniem liczby 7t. Dostajemy stąd, że Atc musi być mniejsze niż ok. 0,00016, czyli nie wystarczy użyć popularnego przybliżenia 3,14, powinniśmy użyć przybliżenia liczby k z dokładnością przynajmniej do 4 miejsca po przecinku lub lepszego.

Literatura

[1]    A.Januszajtis: Fizyka dla politechnik, t.l. PWN, Warszawa 1977, s.222 i n.

[2]    T.Dryński: Ćwiczenia laboratoryjne z fizyki. PWN, Warszawa 1967.

Ćwiczenie 2 *

Wyznaczanie momentów bezwładności ciał sztywnych metodami: wahadła fizycznego i torsyjnego

1. Wprowadzenie

1.1. Wahadło fizyczne

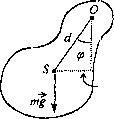
dsinp '

Wahadło fizyczne jest to ciało sztywne o masie m podparte w punkcie O powyżej środka ciężkości S, w odległości d od niego (rys.l). Poniżej udowodnimy, że ruch takiego wahadła odchylonego z położenia równowagi o niewielki kąt (p {ę< 5°), poruszającego się pod wpływem siły grawitacyjnej, można z dobrym przybliżę- Rys.l. Wahadło fizyczne niem uważać za ruch harmoniczny.

Na wahadło fizyczne o momencie bezwładności Iq względem punktu O działa moment siły Mq pochodzący od siły ciężkości mg o wartości:

Mo = -mgd-sinę? .    (1)

Znak (-) oznacza, że moment ten kieruje wahadło do położenia równowagi.

Dla małych wychyleń (ę< 5°) sinę &ę, a więc wzór (1) przyjmuje postać:

Mo = -mgd-ę - -D-ę,    (2)

gdzie: D - mgd jest momentem kierującym.

Pomiędzy momentem siły Mo a przyspieszeniem kątowym(£ = ę) zachodzi związek:

lo-s = Mo.    (3)

Podstawiając wzór (2) do (3) otrzymujemy:

Opracował A.Kubisz.