skanuj0108

prostokątny (rys. 8.4c). W momencie końcowym w całym przekroju pręta skręcanego występuje naprężenie styczne o wartości z = z_pl.

Przejście z trójkątnego rozkładu naprężeń do prostokątnego spowodowane jest tym, że z chwilą osiągnięcia w zewnętrznej warstwie próbki granicy plastyczności naprężenia te nie zmieniają swej wartości aż do momentu, gdy zostaną wyrównane wartości naprężeń w całym przekroju- Dla takiego stanu naprężenia otrzymuje się proste wyrażenie na moment M_pl w funkcji naprężeń t_pl:

^MPi = KpdF

F

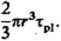
(8.10)

Przyjmując współczynnik bezpieczeństwa

AL

(8.11)

z zależności (8.10) otrzymujemy prosty wzór na długość promienia pręta skręcanego:

r =

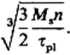
(8.12)

Wyznaczona ze wzoru (8.12) wartość r jest około 9% mniejsza od wartości promienia wyznaczonej dla tego samego przypadku ze wzoru (8.9).

Wzór (8.12) można stosować tylko wówczas, gdy:

—    obciążenie pręta jest statyczne,

—    stanem niebezpiecznym dla materiału pręta jest stan pełnego uplastycznienia.

82. CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie modułu sprężystości postaciowej G materiału próbki o przekroju kołowym przez pomiar jej kąta skręcenia.

Ze wzoru (8.7) otrzymujemy:

M /

G = —^MPa,    (8.13)

<f>*o

gdzie M_s N-m jest momentem skręcającym próbkę, l_p m - długością pomiarową próbki, q> rad — kątem skręcenia odcinka pomiarowego, /₀ m⁴ — biegunowym momentem bezwładności przekroju próbki.

131