skanuj0160

ł

Ćwiczenie 29*

Wyznaczanie prędkości dźwięku w powietrzu

I. Wprowadzenie 1.1. Fale mechaniczne

Fala to zaburzenie lub zespół zaburzeń rozchodzących się w przestrzeni, które mogą mieć postać impulsu lub drgań. Jeśli pewien fragment ośrodka materialnego zaczyna drgać wokół położenia równowagi, to dzięki sprężystym własnościom tego ośrodka drgania są przekazywane sąsiednim fragmentom i zaburzenie rozchodzi się jako fala mechaniczna.

kierunek propagacji fali przemieszczenie V^-V

Rys.l. Podłużna fala mechaniczna rozchodząca się w sprężynie. Ruch ręki powoduje ściskanie i rozciąganie zwojów

Fale dźwiękowe zaliczamy do podłużnych fal mechanicznych, ponieważ materialne cząstki ośrodka, którym może być ciało stałe, ciecz lub gaz, drgają wzdłuż kierunku propagacji fali (rys. 1). Jeśli ruch cząstek odbywa się prostopadle do kierunku rozchodzenia się fali, mówimy o fali poprzecznej (rys.2.). Jej przykładem jest zaburzenie rozchodzące się w strunie, której jeden koniec /ostał wprawiony w drgania.

Do opisu fal stosujemy funkcje falowe ip{x,y,z,t). Jeśli fala rozchodzi się wzdłuż osi x, to dla określonego punktu ośrodka (zadana wartość x) funkcja falowa opisze jego wychylenia w czasie, np. drgania ustalonego elementu

' Opracowała: dr Barbara Oleś

u

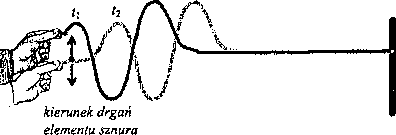
Rys.2. Fala mechaniczna generowana w sznurze przez poruszanie jego końca w górę i dół. Ukazany jest kształt sznura w dwóch chwilach czasu (j oraz t₂ > tj. Ruch elementów sznura jest prostopadły do kierunku rozchodzenia się fali stąd mamy do czynienia z falą poprzeczną

sznura zaznaczone strzałką na rys.2. W szczególnym przypadku, gdy każdy element ośrodka drga ruchem harmonicznym prostym, tj. opisanym funkcją y/(t) = A sin (2jt ft + ę), gdzie A - amplituda drgań, / = 1 / T - częstotliwość, T -okres, ę— faza początkowa (patrz rys.3a), to mamy do czynienia z fala harmoniczną. Z kolei ustalając czas t dostaniemy informację o wychyleniach cząstek ośrodka wzdłuż osi x jak na rys.3b. Zauważmy, że przedstawiona na nim fala harmoniczna ma kształt sinusoidalny i cechuje ją okresowość przestrzenna. Odległość, między dwoma najbliższymi punktami przestrzeni, w których fazy funkcji y danej chwili t są identyczne, nazywamy długością fali X. Jeśli prędkość rozchodzenia się fali wynosi v, to zachodzi: X = uT, gdzie Tjest okresem, czasem w którym fala przebiega odległość równą X.

Funkcja falowa fali harmonicznej może być zapisana w postaci:

Y(x, t) = A sin

— (x + ut) +

A

.. (2k _ 2n - ;4sm —x + ■—•/ + <p

X T

(1)

gdzie znak odnosi się do fali rozchodzącej się w prawo, a „+” w lewo, A jest amplitudą fali, ę- fazą początkową. Wzór (1) przyjmie zwartą postać, jeśli wprowadzimy nowe wielkości, liczbę falową k-2nlX oraz częstość kołową a = 2%!T = 2nf :

y/(x, t) = A sin (kxTcot + <p). (2)