skanuj40001

8

u) Opornik idealny (rczysttmcjn R)

W przypadku elementu czysto rczystancyjnego prąd jest u fazie z napięciem, k:\t przesunięcia fazowego ip jest lówny zero.

U = U_m ■ sin GM I - I- SIU GM

Moc chwilowy otrzymamy:

P = u • i = U_m • l_m • sin² co(

a po uwzględnieniu zależności trygonometrycznej:

•    2    t 1

sin 0)1 =---coslcat

2 2

oraz

U_m = i /_w = /v'2

Zależność na moc chwilową przyjmuję postać:

p = U • l - U ' I - cos 2 co/.

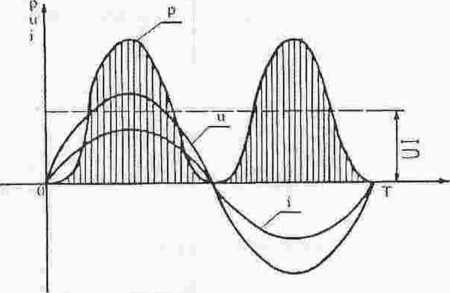
Prąd i napięcie mają zawsze te same znaki, a więc moc chwilowa jest stale nieujemna (wykres mocy nad osią czasu): element R pobiera moc ze źródła w każdym przedziale czasowym.

- Moc czynna wydzielona na elemencie rćzystancyjnym .jest równa średniej wartości mocy chwilowej za jeden okres:

p =    = lj _pdt = -\Wdl - -J W cos 2-cotdt-U-I

*4    * i T o

u ponieważ U = l F< (dla elementu R)

P = I²-R

- Powierzchnia zakreśkowuna jest proporcjonalna do energii elektrycznej dostarczonej do obwodu, zamienionej na energię cieplna w ciągu okresu

T

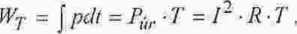
0

natomiast, określona w czasie li będącym całkowitą wielokrotnością okresu lub pólokresu nazywa się energią czynną pobierana w tym czasie przez odbiornik rezystancyjny

W_R = I² ■ R • ty = P ■ ty

- Wykres wektorowy przy obciążeniu rezysuneyjnym

Kąt przesunięcia fazowego >p =0, prąd jest w fazie z napięciem, a więc jest prądem czynnym.

- Moc czynna, bierna i pozorna wyznaczone z zależności ogólnych

P — U • I ■ COS (p — U‘I. bo dla </> - 0. cosę» /

W tym przypadku moc czynna jest równa mocy pozornej:

S = UI

moc bierna:

O — U • I • sitl (p — 0. bo dla <fl = 0. siiup - 0

b) Cewka idealna, chimiktetyzującu się wyłącznie indukcyjnością (element typu L)

W cewce idealnej poddanej działaniu wymuszenia sinusoidalnego przebieg wartości chwilowej napięcia wyprzedza w fazie o 90*’ przebieg wartości chwilowej prądu, lub leż (co jest równoznaczne) przebieg wartości chwilowej prądu opóźnia się w fazie o 90" względem przebiegu wartości chwilowej napięcia.

/ = /„, • sin cot

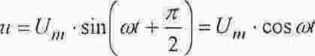
- Moc chwilowa:

p =u‘i = tJ_n, • I_m ■ sin cot • coscot