skanuj40001

8

u) Opornik idealny (rezystancja R)

W przypadku elementu czysto rezystancyjnego prąd jest w lazie z napięciem, kąt przesunięcia fazowego tp jest równy zero.

u = U,„ -sincoł

I - I_m - SIU Ml

Moc chwilową otrzymamy:

/? = «•/= U_m • l_m 'Sin²^ a po uwzględnieniu zależności trygonometrycznej:

•    2    t 1

sin cal----zoslco!

2 2

oraz

U_m = u-S i /„, = /• V2

Zależność na moc chwilową przyjmuję posiać:

p- U • I - U • f ■ cos 2(oi

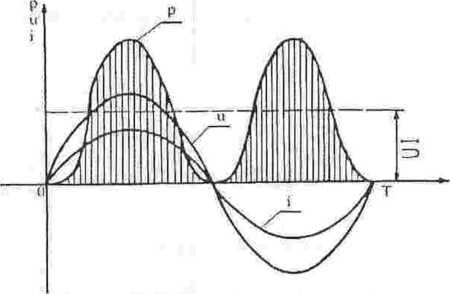
Prąd i napięcie mają zawsze te same znaki, a więc moc chwilowa jest stale nieujemna (wykres mocy nad osią czasu); element 11 pobiera moc ze źródła w każdym przedziale czasowym.

- Moc czynna wydzielona na elemencie rezystancyjnym jest równa średniej wartości mocy chwilowej za jeden okres:

j T    i T    i 7

P = P_fir = pdt = -\Uldi—_:JUl cos Icotdi = U-I

i a    n    7 o

a ponieważ U=l K (dla elementu R)

P = I¹ R

-    Powierzchnia z akre skowana jest proporcjonalna do energii elektrycznej dostarczonej do obwodu, zamienionej na energię cieplna w ciągu okresu

T

W_T = \pc/t=P_th.-T = I²R-T. o

natomiast, określona w c/a-sie t| będącym całkowitą wielokrotnością okresu lub pólókresu nazywa się energią czynną pobierana w tym czasie przez odbiornik rezystaneyjny

W_R = I² *R.l_x=P‘l_x

-    Wykres wektorowy przy obciążeniu rezyslaneyjnym

Kąt przesunięcia fazow ego <p -fi prąd jest w fazie z napięciem, a więc jest prądem czynnym.

• Moc czynna, bierna \ pozorna wyznaczone z zależności ogólnych

P = U' • I • COS (p — U • /, bo dla i/> - 0. cosył /

W tym przypadku moc czynna jest równa mocy pozornej:

S = u-I

moc bierna:

O = U • 1 • sili (p — 0. bo dla </> - 0, smtp - 0

b) Cewka idealna, charakteryzująca się wyłącznie indukcyjnnścią (element typu L)

W cewce idealnej poddanej działaniu wymuszenia sinusoidalnego przebieg wartości chwilowej napięcia wyprzedza w lazie o 90" przebieg wartości chwilowej prądu, lub też (co jest równoznaczne) przebieg wartości chwilowej prądu opóźnia się w fazie o 90" względem przebiegu wartości chwilowej napięcia.

/ = I_m • sin (Ot

( 7t ^ (Ot + —

l

u - U,,, ■ sin

= U_m • cos o)t

■ Moc chwilowa:

p —u-i = lJ,_n • /_n, ■ sin (ot • cos cot