wm zad2 rozciaganie

ROZCIĄGANIE

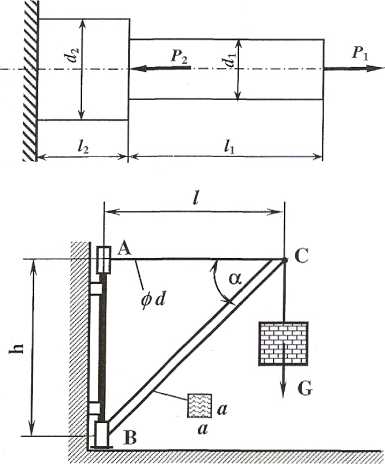
1. Dla pręta jak na rysunku o wymiarach. d$=20 mm, /i=0.8 m, i₂=40 mm, /₂=0.4 m, obciążonego silami Pj=20 kN i P₂= 40 kN, wykonać wykres sil normalnych (N) oraz obliczyć naprężenia rozciągające w przekrojach obydwu średnic (g_1? g₂). Przyjmując, że pręt wykonano ze stali dla której moduł Youńga E=2.05*I0^{1 2} MPa oraz liczba Poissona v=0.26 obliczyć całkowite wydłużenie pręta (A/_c) oraz wymiary średnic po obciążeniu (di, d₂).

2. Na konstrukcji żurawia obrotowego złożonej z drewnianej podpoiy BC i stalowej liny AC podwieszono ciężar G=l,5 kN. Określić średnicę pręta (d) oraz wymiar przekroju kwadratowego podpory (a) jeżeli dopuszczalne naprężenia rozciągające dla stali &_r=160 MPa a ściskające dla drewna k_c=5 MPa. Wartość kąta ce=45° (/=h).

3. Pręt stalowy o średnic}' d-32 mm poddano rozciąganiu osiową siłą iV=135 kN. Przy tym obciążeniu zmierzono pomniejszenie średnicy pręta o A/f=0.0062 mm oraz na długości pomiarowej /=50 mm zaobserwowano wydłużenie o A/=0.04 mm. Określić moduł sprężystości (E) i współczynnik Poissona (v) dla materiału pręta.

1

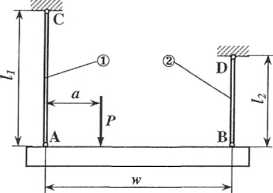
Sztywną belkę AB zawieszono na dwóch cięgnach o przekroju okrągłym odległych od siebie o w=2000 mm. Cięgno 1 o średnicy */i=20 mm oraz długości /i=1500 mm wykonano ze stali (£j=2*10² MPa), zaś cięgno 2 o średnicy d₂=25 mm i długości /₂⁼1000 mm zostało wykonane z miedzi (I?₂=l*10² MPa). W jakiej odległości a od węzła A należy przyłożyć siłę P aby po odkształceniu cięgien belka

2

pozostała pozioma? Wyznaczyć naprężenia w obu cięgnach (Oi, o₂), oraz pionowe przemieszczenie belki (A/) jeżeli P=30 kN.