zdjecie0023

25

2 przećhodnioścl nierówności wynika, te a < b    dla n> a «

Twierdzenia 1.9. Jetell 1. 11* a_Q - a,2. lim b_Q - b i 3. a_Q^ b_n

n-c-co    n-*co

dla n> n^, to a^. b.

Dowód. Dla dowodu nie wprost przypuśćmy, te a <b. 2 twierdzenia '■ .8 wynika, te istnieje Hj takie, te dla nr- n. a_Q< b_n, a to Jest sprzeczne z założeniem 3. Twierdzenia 1.8 i 1.9 noszą nazwą twierdzeń o monotonii. Twierdzenie 1.9 orzeka, te nierówność słaba zachowuje 8lę w granicy. Nierówność nocna mote się w granicy nie zachować. Na przykład dla każdego naturalnego n spełniona Jest nierówność nocna

lin (-1) n—<o

natomiaot

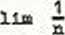
n-KD

0

Twierdzenie 1.10 /o trzech ciągach/. Jetell

lim a - lim c - g, u    n

n-*o?    n-*o)

a ponadto istnieje taka liczba n,, że dla każdego n> a, spełniona

Jest nierówność a .< b .< c , to n - n *- a

lim b_n - g n—-cr>

Dowód. Niech £ będzie dowolną liczbą dodatnią. Ponieważ lim a - g,

n-*eo

więc istnieje taka liczba    ic

dla n> n₂ ;

| a_n - g I < e

w szczególności

g - £ <

dla n > n₂ •