014 3

rlM

j—^

zz:

Algorytm

mirwmołizOC)l

wskażn.ta

jokoici

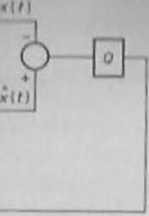
Kw I ■* S lu nuu blokowy procentu estymacji parametrów modelu / wykorzystaniom algorytmu

dostrajania modelu

S‘ hemat procesu identyfikacji przy zastosowaniu algorytmu dostrajania modelu przedstawiono na rys. 1.9.

Metody estymacji, których algorytm opiera się na wyżej opisanych zasadach, kird/o często s.i nazywane metodami iteracyjnymi lub metodami estymacji z modelem u. . .Ksm się Metody te szeroko wykorzystuje się w automatyce, a w szczególności w sterowaniu adaptacyjnym. Ze względu na swoją uniwersalność znajdują one coraz szets/c zastosowanie w identyfikacji układów mechanicznych.

1'tzcgląd metod dostrajania modelu oraz problemów związanych z ich stosowaniem przedstawiono w rozdz. 7. Do najistotniejszych należy problem jednoznaczności w w .t wnow.mych parametrów, związany z występowaniem minimów lokalnych i ęloh.ilnych założonego kryterium jakości, szczególnie w przypadku estymacji l> n.imctiow modeli nieliniowych.

/ zastosowaniem jednej z reguł estymacji parametrów wiąże się zawsze problem blolnw Wędy popełnione na etapie estymacji, nazywane błędami estymacji, można i * • 1 • o In na błędy systematyczne i losowe. Błędy systematyczne są zw iązane / zasii .ow.imcm pewnych uproszczeń lub przybliżeń, których przyczynę stanowi kou.ilosć stosowanych metod obliczeniowych. Błędy te w prosty sposob mu nu " zacować i wyeliminować z rozważań. Błędy losowe związane są / Wędami • >hi -u i błędami wniesionymi do procesu estymacji przez dane z pomiarów.

I ik*•.. ofi/ymunych estymatorów ocenia się badając ich podstawowe cechy obi lą/oność,

''godność,

efektywność.

dostttteczność.

i .i .m iim ust obciążony, jeżeli

E    (1.21)

gd.-u- I J ;    operator'wartości oczekiwanej, fi estymator parametru modelu.

!< dokładna wartość parametru.

k i i/M h.

•    i" i i< im ii> życie) błędem systematycznym.

•    m i< i .......Inv jczch dl.i rosnącego czasu estymacji / zachodzi związek

11.2 M

lim Pd/? b\ > i. | o

4» •• •• nm/a v wartość estymatora jest zbieżna według prawdopodobień i n u mi , i iitti ludne)

iflMo.u /I jchI elcklyw ny. jeżeli dla każdego nieobciążonego estymatora // jest m • Muiownon

M/i| 'il/i »]t^-^fc]^łl«Ei[/r /.][/T-h]⁷ = c..vt/ri. o24)

11 lin/tuu/.i ze estymator jest efektywny.jeżeli ma najmniejsza wariancję i rtd i>l> ni*-•ibciit/onycli estymatorów badanych parametrów.

I o fMui.u /' i< st dostateczny, jeżeli dla wszystkich innych estymatorów jl.

! » uaiiości dokładnej h.

ftphiiMho . Ntymaloi powinien być: nieobciążony. efektywny. zgodny i dostatecz powzależności są spełnione tylko dla T > /' : wtedy mówimy • im li a.wnptotycznych estymatorów.

^t naklei \ styk.j statystyczną estymatorów jest funkcja gęstości prawdo po *•!%*.» r»lsmatoi,i, która jednak ze względu na trudności obliczeniowe u* >* tt w>koi/\slywana do oceny jakości estymatorów. Przedstawione wyżej po-tln łonu i- dymacji oparte jest na określeniu funkcji jakości modelu.

Ihmom i- .1. i.. icm do estymacji jest podejście statystyczne, w którym bardzo ważną |d|i\wa «Iv ,ponowami wiedza a priori o obiekcie. W zależności od rodzaju tej i tic się m/ne. optymalne w każdym przypadku, procedury estymacji Nilfittun informacji a priori jest wymagane przy stosowaniu estymaloia uai >•(« kwadratów Wystarczy tu stwierdzenie, że struktura przyjętego modelu i.mm.i.i iMikimzc obiektu

................. jest estymator Markowa Jego zastosowanie jest możjiwc

|| i-tdku. gdv dodatkowo dysponuje się informacja o wartościach elementów ttfttf*¹¹ k"wana,n<.ji s/umu

Imir^ wąi'1 mlormacji a priori o obiekcie należy mieć przy stosowaniu

CnWMi.ua u.i|wlększe| wiarygodności, jest tu. mianowicie, wymagana znajonn»w k li mmm - i prawodpodobicństwa procesu, micr/onego na obiekcie, na podstawił |t i‘ »>.' pi. • pntwad/a się estymację.

Nh|vsh• * i wiedzy a priori o obiekcie musimy posiadać przy stosowaniu esty

C*...... u* ..i I* h .losowanie wymaga znajomości funkcji gęstości piuwdopndn

ii • \« i z• • uvi li paramrtiow oraz kosztów spowodowanych błędami /ak l.ul.i|.o

m*im i m.I . a priori otrzymamy inne estymatory jako pizypadki •*/.« zrgólnr >*•1 * Minlmtiw Iłayesa