029(1)

97. lim (i/jr+je+1 — ) .v²-jc+1)    98. lim

X -**4-00

99. lim ,v(| ,x²+1 —x)

u³+4i/²-|-4w 101. lim —4--L_.

(/_►—2 U —U—O

sin ax •o tg 6.v

100. lim ^Sin<Jt+¹⁾

l-^²

102. lim--¹ — * cos 2x *-T

103. |_im sio («+/■)- Si. (*-*)

A->o    /*

105. Jim i i -(-sin x

3T-.0 '

arc cos —

104*. lim — ——

*_₂-o x—2

^    x⁴-18^+81

106. lim

I" 2x²-3x-9

M

JOT*. Hm£-^,£ -*+1 _p_2    p-—2p-+3p-6

109*. lim sin 3.v ctg 5x *-.0

tu*, lim 'jSL

.Ty 2^4“ i

£

113. Jak zachowują się pierwiastki xi oraz x₂ pełnego równania kwadratowego ax²\-bx-\-c — 0, gdy współczynnik a -» 0 (b ^ 0, c — stałe)?

108. lim 17—3    .

.    I2x-5\^X~¹

112*. lim (sin jc)‘**^x

110. lim

x-+oo

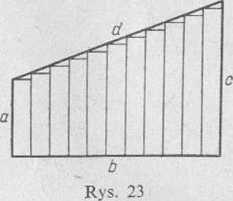
114. Prostokątny trapez podzielono prostymi równoległymi do jego podstaw na « równych co do wysokości, małych trapezów, a następnie w każdy z nich wpisano prostokąt (rys. 23). Jak zachowuje się pole S_n i obwód P„ otrzymanej w ten sposób schodkowej figury, gdy n -> -f-00?

Celem porównania dwóch nieskończenie małych wielkości a i /?, znaj-lujemy granicę ich stosunku. Przy tym:

1) jeżeli lim = 0, to mów imy, że rząd nieskończenie mulej z jest wyższy liż rząd nieskończenie malej fj;

2) jeżeli lim ~ = oo, to mówimy, że rząd nieskończenie malej ot jest niższy •liż rząd /?;

3)    jeżeli lim * = A (A ^ 0, A ^ co), to mówimy, że nieskończenie małe z i fi są tego samego rzędu;

4)    jeżeli lim y = 1, to nieskończenie małe wielkości ot i fi nazywamy równoważnymi. Równoważność nieskończenie małych wielkości a i (i oznacza się symbolem przybliżonej równości ot s; fi.

Równoważne wielkości nieskończenie małe mają następujące własności: 1. Różnica dwóch nieskończenie małych równoważnych jest wielkością nieskończenie małą o rzędzie wyższym od każdej z nich.

IT. Przy poszukiwaniu granicy stosunku dwóch wielkości nieskończenie małych można każdą z nich (lub tylko jedną) zastąpić inną równoważną wielkością nieskończenie małą, tj. jeżeli a z oti oraz fi X pi, to

lim

= lim - ‘ = lim = lim

^ai

P

Pi

Pi

115. Jeżeli x -> 0, to które spośród poniższych nieskończenie mały ch wielkości: 1) 10x, 2) a-³, 3) ] 3x, 4) tg 5) Ig(1-for) są wyższego rzędu niż

które są rzędu niższego, a które są tego samego rzędu?

Rozwiązanie. Znajdujemy granicę stosunku każdej z danych nieskończenie małych i nieskończenie małej x.

1)    lim — = 10

-v-*-0 X

^a więc 10x jest nieskończenie małą tego samego rzędu, co x.

2)    Jim = lim x² = 0

x~±0 X

czyli a-³ jest nieskończenie małą rzędu wyższego niż x.