065(1)

i

Podstawiając * = arc 49° = • y^- - i a = arc 45° = - ^ , otrzymamy

i

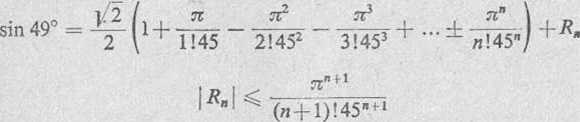
Aby określić, ile wyrazów początkowych należy uwzględnić dla zapewnienia wymaganej dokładności rachunków, szacujemy wielkości kolejnych reszt R„

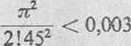
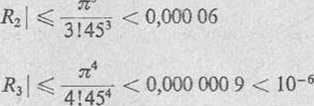
Widzimy, że żądaną dokładność obliczeń można osiągnąć, jeśli weźmiemy cztery początkowe wyrazy wzoru, poprzedzające R₃

sin 49° s;

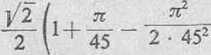
6 ■ 45³

X 0,707 106 8(1+0,069 813 1-0,002 436 9-0,000 056 7) a « 0,754 709

(wartości n, y 2 i wszystkie wyniki działań pośrednich pisane są z nadmiarem jednego miejsca dziesiętnego, tj. z siedmioma miejscami dziesiętnymi).

Wartość sin 49° można też obliczyć na podstawie wzoru Maclauriną dla funkcji sin*, ale wtedy, aby osiągnąć żądaną dokładność trzeba uwzględnić znacznie więcej wyrazów tego wzoru.

3) Dany pierwiastek zapiszemy w postaci

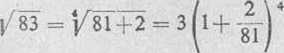
i zastosujemy uogólniony wzór dwumianowy Newtona (4), otrzymany przy rozwiązywaniu zad. 303.

2 .    i

Podstawiając / = gy i/n = j, otrzymamy

V^A83 3 |l+:_;162    i₆2 . 108 ⁺

162 • 108 ■ 486

+ +R_n

162 • 108 • 486 • 54 Szacując wielkości kolejnych wartości 3!2?_nj, znajdujemy

3

3|J?,|<

3|Ri\ <

3|J?j| <

162 • 108 3 ■ 7

162 • 108 • 486 3 • 7

< 0,000 2

< 0,000 003

< 0,000 000 06

162 • 108 • 486 ■ 54

Aby więc otrzymać wynik obliczeń z daną dokładnością, wystarczy wziąć sumę czterech wyrazów wzoru dwumianowego, poprzedzających resztę R₃

1^83 as 3(1+0,006 172 8 - 0,000 057 2 +0,000 000 8) X 3,018 349

4) Przekształcamy dany pierwiastek

y-i2i-v 125-4=5(1-+)

i podstawiamy do wzoru dwumianowego t — — yyj = — 0,032 oraz m =

= 4-. Otrzymamy

⁸/l2T=5|l-^

0,032²    5 • 0,032³    10 > 0,032⁴

3    9    81    243

Badając kolejne wielkości błędu 5 _i R„\, znajdujemy

— ... +i?„

l/l !	\i ^1 2	\/l 3\
	\ 3 “^2	II3 ^3I

4!

- 0,032+1 —0,0320)

7--3-1

³ < 10-⁵

133