25(2)

Przykład 5.4

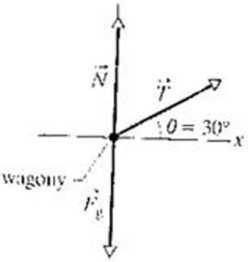
Powróćmy temz do Johna Massisa i u agonów kolejowych. Za-lozmy. że Massis ciągnął koniec liny (zębami) ze stałą silą. więk-sm) 2.5 razy od swego ciężaru. pod kątem H równym M) _lio poziomu. Jego masa ni wynosiła 80 kg. Ciężar W wagonów był am ny 700 k.\\ a Massis przesunął je po szynach na odległość I m. Przyjmijmy, że koła wagonów poruszały się po szy nach bez oporu. Me wynosiła prędkość wagonów, gdy Massis przestał jo ciągnąć?

ROZWIĄZANIE-

1. /.drugiej zasady dynamiki Newtona wyniku, że wagony pjiriisznłj się ze Małym p.zysp.es/cn,e.n poziomym. edvż Massis etągnął je ze Małą siłą ,H»ziomą. Przyspieszenie jest stałe, a ruch akJkkI/i w ,ednycn wymiarze, dlatego też do wv/nae/enia prędkości r wagonów, po pr/el>>c»«. przez nie drogi ,/ ., \ _m„ż,.a zasloMAcac równania z c.heli 2.1. iW/chnc jes. równanie zawierające r Spróbujmy zastosować równanie (2.16):

»•    — « n i- 2tt( r    (5.15)

przyjmując. ze oś i jest zgani,u / kierunkiem ruchu, jak na piyod sław uijąeym d.agram s,ł rysunku 5.11. Wiemy, że prędkość ,*>. e/ątkowa r„ jes. równa o. przemieś a zonie    wenosi <f

m. Nie znamy jednak przyspieszenia«/ wagonów w /dłuż os, .t.

’ ²- ^Preys,’^icSi'^c,,ic « je« związane / siłą il2iat.ij._Xa „ gony 2c strony liny. a związek ,c„ jes, „pisany _Za

zasatly dynamiki No winna. Ola składowych    _<„.^4dn‘

sunkn y|| ma ono posiać:    _tzv|_i:    ' ¹

^npi — tn_wu.

(5.

P czym /«„. jest masą wagonów. Jedyną siłą działająca n-, ^ony w kierunku poziomym jest składowa pozioma TcęTn prężenia T liny ciągniętej przez Massisa. Wobec ic>o rów ^ O-1 C») przybiera posiać:    * ^f0Wn^

7 cosO = ni_na.

<517) •.

Wjcoiy. ic r jcsl 2.5 razy większe ud ciężaru Massis, ,. i

^W>"^,ka " <^{5 121}«*    rdwoy a za.en, ^ f

/ = 2.5mx = (2.5)|S0 kg)(‘).x m/s-j: l<»r,t) \

Jos. I„ Siła. jak;, wykazuje się dobry ciężarow iec średniej w i •» więc bynąimmej nie jest ona nadludzkiej wielkości.    1

.. ^Ahy    " * równania <5.17) mus,my jesze/c o|,il

c/u/«.*. tym celu skorzystamy znów / nnuiania <5.12) i_Xw| Mawia/ąe do mego tym razem ciężar U wagonów

_ ^l‘‘    (7 l()⁵i\)

“ 7 ^{=    = 7,143}' ^m‘ ^k*

^eksznilcajac rów;.....nic (5.17, i postawiaj,,,: war,ości liczbowe

• •^,n* ¹ " oir/yimijcmy:

Rys. 5.11. Przykład 5 4 Diagram •sil dla w agonów osobowych ciągniętych przez \lassisa. Wektory nre są narysowane w skali: siła T działająca na wagony ze strony linv jest znacznie niniejsza od \d_\ iw».-walnej, działającej na wagony /e słttmy szyn i d/inlająccj na wagony Niły ciężkości /

v

/ eos «

(l⁴>60 Nl(cos M) j

= 0.»237(i jn/s-.

(7. M3 - 10* kg>

WMawKijąc tę wartość - oraz inne wartości znane - do wzoru (5.15). dostajemy:

f² •-<> + 2(0.02376 m/s-><] m)

czyli

f — 0.22 m/s.    (odpowiedź)

^    % do wagonu

y zcj. tak aby była ona pozioma. Czy wiesz dlaczego-'

książka A    j pudło/*

trzecia zasada dynamiki Newtona

u)

^KP

K

o-

r

/*k

W

Rys. 5.12. n) Książka K opiera się o pudlo P. b) Zg<xlnic z trzecią zasada dynamiki Newtona siła ?_Kr. jaką pudło działa na ksią/kę. ma taką samą wartość i przeciwny kierunek jak siła ]',._K , jaką książka działa na pudlo

Ody dwa ciała odpychają się lub prż.yciągąją, _t/n. gdy każde z nich d7iala na

książkę A n.i polce tak, iz opiera się ona o pudlo P (rys 5 I2vi le.iJr- •„ „ odmalują Wicdy ze sobą: istnieje siła pozioma F_K„. jaką pudło działa na k^ążkę

na y nlfu'" I2b Tr'^    ^    ^ ^{Te (iwie} ^ P' -ds.awiono

^{y nku} 5A2b' ^{Trzcc,a zasat,a} dynamiki Newtona mówi, że:

^ Trzecia zasada dynamiki Newtona Gdv dwadih    •

działają one na siebie mają laką samą war,ość bezbłędną i £££ kier^kf

-książki i pudła możemy tę «sadę zapisać jako równanie skalarne:

^a    _ y_pK    (jednakowe wartości bezwzględne)

równanie wektorowe:

-    _ —Fnf    (jednakowe wartości bezwzględne i przcewne kierunk,).

~^Ke _znak minus oznacza, że siły mają przeciwne kierunki. Sity te nazy-„ akcii i reakcji (parą akcja-reakcja). Takie, dwie siły występu*

J ^S' . dwa ciała oddziałują ze sobą i to w każdych warunkach. Książka ^C’ ° rvsunku S !2a sa nieruchome, lecz trzecia zasada dynamik, Newtona wówczas! gdy ciała są w ruchu, a nawet wtedy, gdy poruszają

melona leżącego na stole, który stoi na 1 Ha) i znajdźmy związane z melonem siły akcj, , reakcji. Melon ze stołem, a także z Ziemią (mamy więc do czynienia z trzema calami.

oddziaływania .mtómy    ~‘^_s. _5J,_h). siła / „> jes, ui sila

^.niemY sie naipiei w samym mwonem v*

rtka slól działa na melona, a sita F,,x to siła ciężkości, jaką Ziemia

Ha ns'melona. Czy jest to para akcja-reakcja? Nic. ho są ,o siły działające ^dZ    lo - melona - a nie na dwa ciała, oddzi,dujące k. sot'<ł-

^naCyzu.leżć parę akeja-rcakeja. musimy zająć się nie melonem, lecz od-z    meL z jodnsan z dwóch pozostałych ciał. Rozważmy na,pierw

oddzfalywanic melon-Ziemia (rys. S.Uc). Ziemia przyci^.

«cvina Fuz a melon przyciąga Ziemię siłą grawitacyjną F,». Czy jest pm. lh-reakeja- Tak. są lo siły działające między dwoma oddziałującym, ze sr ą

dynamiki Newtona:

— —F/m    {oddziaływanie nicłon-Zicmia).

Ponadto w oddziaływaniu molo,,, stół stół działa na melona tół, ^ działa na stół siłą h,, (rys. 5.1M). To także jest para akcja-reakcja ■ analog.cz.

manty:    „

jr_sl!f —/ _vw    (odti/.iaływanic tnoUm—Mol,.

kierunki?

5.8. Jak stosować zasady dynamiki Newtona?

Pozostała część tego rozdziału zawiera same przykiady. Howmieneś się w nie zaglębić, aby poznać nie tylko konkretne odpowiedz,, lecz przede wszystkm n tody^rozwiązywania tego typu zadać. Zwłaszcza ważne jes, ,0. tóyjjtó W od szkicu sytuacji fizycznej do diagramu sil w dobrze dobranym układzie współ umożliw, zastosowanie zasad dynamiki. zadania, które rozwiążemy bardzo szczegółowo, korzystając ze schcm. py •

i odpowied/i.

melon M

7-ierrua Z

a)

stół 5

^P,_fS (sił;, normalnu /o strony stołu)

'u

I r._u7 (sił;» ciężkości)

b)

melon

j/irz

|fzr,

Zicmiii

c)

.*

l'Ms

r

SM

d)

Rys. 5 13. .0 Melon loży na Molo. kiói> stoi iw Ziemi, h) Siły d/.iahijącc nn nu-łono: his i hf/.- ^ ^P*^{,ra akc}i^;*' ^icakc’^l,: oddziaływanie niclon-Zicmia. il) Pm u akcja-reakcja: oddziaływanie inelon-MÓł

100

5. Siło i ruch I

5.8. Jok stosować zasady dynamiki Newtona*