2027

LABORATORIUM © AM 1)2009

Laboratorium Elektrotechniki i elektroniki

Temat ćwiczenia-'

POMIARY OSCYLOSKOPEM OKRESOWYCH PRZEBIEGÓW CZASOWYCH

Symulacja komputerowa

Wyznaczenie wartości skutecznej i średniej sygnałów okresowych

Ćwiczenie n^la za zadanie zapoznanie studentów z pomiarami oscyloskopem przebiegów (sygnałów) czasowych, działaniem generatora funkcyjnego oraz pomiarami multimetrem prądów i napięć w trybie IX' i AC. Na podstawie pomiarów oscyloskopem należy wyznaczyć wartości średnic i skuteczne badanych przebiegów okresowych i porównać obliczone wartości z wartościami zmierzonymi przyrządami pomiarowymi-

Przebieg okresowy można zapisać jako funkcję ffO^fO+tiT), gdzie: T okres podstawowy (najmniejsza wartość czasu - po upływie, którego funkcja zaczyna się powtarzać), ne N. Parametry charakteryzujące przebieg okresowy to wartość średnia i wartość skuteczna. Poniżej podano wzory definicyjne tych wielkości.

(l)

‘ o

Badane przebiegi okresowe otrzymujemy z generatora funkcyjnego. Między innymi możemy na nim ustawić kształt, amplitudę oraz częstotliwość przebiegu. Przykładowe przebiegi (sinusoidalny, prostokątny i trójkątny) otrzymane z generatora przedstawia rysunek I.

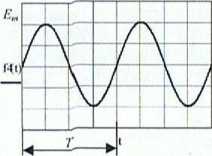
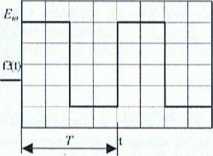
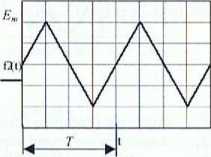
Rys. I. Przykładowe przebiegi sinusoidalny, prostokątny i trójkątny, E„, - amplituda przebiegu dla obciążenia /?«, T- okres sygnału

Dla powyższych przebiegów wartości średnie równe są zero, natomiast wartości skuteczne obliczone ze wzoru (I) odpowiednio wynoszą:

*    .łA-|łfMlokal;i    ¹    ^xk - Irojknlu    ^

Przy pomiarach przyrządami analogowymi, do pomiaru wartości średnich można zastosować przyrządy magnctoelektryczne (ME) a do pomiaru wartości skutecznych stosuje się przyrządy elektromagnetyczne (EM) (amperomierze, woltomierze). Przy pomiarach przyrządami cyfrowymi, IX’ (direct currcnt) oznacza pomiar prądu stałego, a AC (alternating currcnt) pomiary prądu przemiennego. Napis Truć RMS na przyrządzie cyfrowym oznacza prawidłowy pomiar wartości skutecznej przebiegu AC.

Przebieg okresowy można przedstawić w postaci szeregu Fouriera

E,

xk-i<11111 tfoitly

f(/) = F„ + ^ F_mk sin (kun t- <p_k ) = /(„ + £\{A_k cos{ktot) + B_k sin (ktot)),

*-i    *-i

₍₀*1nl T,    F_mk = V A; + B;    cos tp_k = ■ -J*-*--- sin <p_k =    -- F_skk = ~-

V ^Al + Bi    V Ą +    ^2

1 T    ,7’    ,7'

F„ *= 4, = - Jf(t)d/, A_k = - J/(/)cos(/cw/)dt, B_k = - j/(/)sin(Ańrf)d/

'll    'ii    * I)

gdzie: F₀ ' składowa stała

Fmk ^"^ta składowa harmoniczna (amplituda A-tej harmonicznej)

F*k,k - wartość skuteczna A-tcj składowej hannonicznej T - okres podstawowy sygnału

Wartość skuteczną można obliczyć ze składowych harmonicznych według wzoru: F_sk =    + £ F~_{k k} (2)

M *-i

współczynnik szczytu obliczamy ze wzoru: k_s =    (dla funkcji sinusoidalnej /c₍ = v2 )

F*

Funkcje f(t) oraz wzory na k-te harmoniczne dla przebiegu (sygnału) sinusoidalnego, trójkątnego, prostokątnego wyznaczone na podstawie wzorów (1) podano poniżej.

Szereg Fouriera f(t) i składowe harmoniczne dla:

przebiegu trój kątnego

n \    8 F ■łr-1    1

.1(1)-—f y -ysm(A-w/),

ⁿ *-1,3,5 *

dta

k = 1,3,5...

8 F

n'k'

przebiegu prostokątnego

4F

/(0 = —- X 7^sin(Aw/),

^ *.VM ^k

4 F_m n ■ k

dla

k = 1,3,5.

1. Pomiary sygnałów okresowych

W programie Multisim układ pomiarowy należy zestawić zgodnie ze schematem na rysunku I wykorzystując wirtualny generator funkcyjny, oscyloskop dwukanałowy oraz. woltomierz . Dla sygnału sinusoidalnego, prostokątnego i trójkątnego należy dokonać pomiarów oscyloskopem oraz woltomierzem cyfrowym. Na wyjściu generatora funkcyjnego należy ustawić napięcie o amplitudzie w zakresie 5    10V i

częstotliwości 1001 Iz. Wyniki zanotować w tabeli pomiarów. Powtórzyć pomiary dla częstotliwości Ikllz i 200kllz

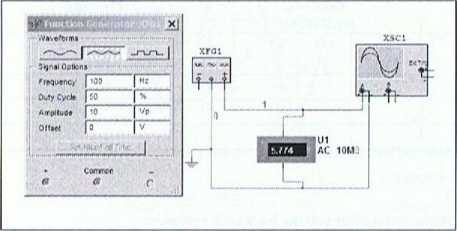
Rys. 1. Schemat układu pomiarowego i przykładowy obraz na oscyloskopie.

U wskazanie woltomierza w trybie AC E,„ amplituda przebiegu T - okres sygnału

Tabela I. Pomiary przebiegów okresowych

l.p.	Częstotliwość	Przebieg sinusoidalny			Przebieg prostokątny			Przebieg trójkątny
		U [V]	Em fV|	T f^ms3	U [V]	Em (V]	r [ms]_	U m	Em [V]	T [ms]
1.	100 [Hz]
2.	1[klIz]
3.	200[kHz]

2

1