388 389

388 Programowanie sieciowe

8.5. Przykłady wykorzystania programowania sieciowego

Przedstawimy trzy różne przykłady wykorzystania metod programowania sieciowego. Przykład 8.4 związany jest z. zagadnieniem sterowania zapasami. Wykorzystując algorytm najkrótszych dróg w sieci, określamy optymalne partie zakupu w kolejnych miesiącach. W przykładzie 8.5 zawarto analizę sieci rurociągowej i opisano, w jaki sposób za pomocą metody maksymalnego przepływu w sieci określić maksymalny przepływ ciepłej wody w systemie ciepłowniczym. Przykład 8.6 dotyczy projektowania sieci komputerowej. Pokazano w nim, jak metoda minimalnego drzewa rozpinającego umożliwia zaprojektowanie takiej sieci.

Omówione przykłady zadań można rozwiązać za pomocą odpowiednich programów komputerowych z pakietu Badania operacyjne z komputerem. "Wersja 2.00 (2003). Inne zadania problemowe i numeryczne z zakresu metod sieciowych zamieszczono na CD-ROM-ie dołączonym do książki.

8.5.1. Dynamiczny problem wielkości zamówienia

Przykład 8.4

Dynamiczny problem wielkości zamówień opisany jest następująco: na początku każdego okresu można złożyć zamówienie w wysokości, która pokrywa popyt z jednego lub kilku następujących po sobie miesięcy. Ze złożeniem zamówienia związany jest koszt stały. Koszty utrzymania zapasu ponoszone są na koniec każdego okresu. Należy określić, w jakich okresach utworzyć zapas i w jakiej wysokości, tak aby zminimalizować łączny koszt zaspokojenia popytu podczas okresu objętego planowaniem. Koszty zakupy są takie same w każdym okresie. Nie ponosimy kosztów utrzymania zapasu w miesiącu, w którym dokonywany jest zakup. Koszt zakupu wynosi 120 zł, jednostkowe koszty utrzymania

Tablica 8.5

Miesiąc	Popyt
i	35
2	70
3	17
4	52
5	42
6	20

zapasu są równe 3 zł niezależnie od długości okresu magazynowania, a popyt w kolejnych miesiącach przedstawiono w tablicy 8.5.

Należy określić optymalny plan zakupów i zapasów dla sześciomiesięcznego okresu planowania.

Rozwiązanie

Konstrukeja sieci

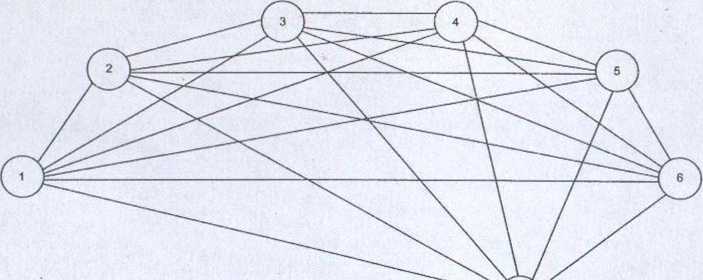
Zadanie znalezienia optymalnego planu zaspokojenia popytu można przedstawić jako zadanie znalezienia najkrótszej drogi od wierzchołka początkowego do wierzchołka o najwyższym numerze w odpowiednio skonstruowanej sieci. Składa się ona z 7 wierzchołków:

wierzchołek I — początek rozpatrywanego okresu, wierzchołek 2 — koniec miesiąca 1, wierzchołek 3 — koniec miesiąca 2, wierzchołek 4 — koniec miesiąca 3, wierzchołek 5 — koniec miesiąca 4, wierzchołek 6 — koniec miesiąca 5, wierzchołek 7 — koniec miesiąca 6.

Wierzchołek 1 jest połączony ze wszystkimi następnymi. Połączenie wierzchołka 1 z 2 oznacza, że złożone na początku pierwszego miesiąca zamówienie będzie pokrywało zapotrzebowanie do końca najbliższego miesiąca. Połączenie wierzchołka 1 z wierzchołkiem n (n = 3, 4, 5, 6. 7) oznacza, że na początku miesiąca 1 złożymy tak duże zamówienie, że zapas wystarczy na zaspokojenie zapotrzebowania aż do końca miesiąca, oznaczonego numerem n. Według tej samej zasady dokonujemy dalszych połączeń. Otrzymaną sieć ilustruje rys. 8.25.

Rysunek 8.25

7