ALG)6

296

RozdziaH3. Kodowanie i kompresja danych

nak jej praktyczna realizacja została opracowana przez R. Rivetsa, A. Shamira i L. Adlemana, stając się znaną jako tzw. kryptosystem RSA. Metoda RSA gwarantuje bardzo duży stopień bezpieczeństwa przesyłanej informacji. Ponieważ została ona uznana przez matematyków za niemożliwą do złamania, stała się momentalnie obiektem zainteresowania komputerowych maniaków na całym świecie, którzy za punkt honoru przyjęli jej złamanie...

Zanim przeanalizujemy system RSA na konkretnym przykładzie liczbowym, spróbujmy zrozumieć samą ideę kryptografii z kluczem publicznym.

Rys. 13 - 2.

jtrj j 117 ;u.AmtujĄpy)

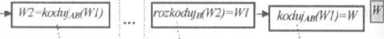
PiCCOdum    Proceduro

prywrfiut

Procedura

piywntna

Piucukm

System kodujący z kluczem publicznym.

System kryptograficzny z kluczem publicznym jest przedstawiony na rysunku 13 - 2. Składa się on z trzech procedur: prywatnych: rozkodujA i rozko-dujB i publicznej: koduje- Nadawca A, chcąc wysłać do odbiorcy B wiadomość IV, w pierwszym momencie czyni rzecz dość dziwną: zamiast „zwyczajnie” zakodować ją i wysłać poprzez kanał transmisyjny do odbiorcy, dodatkowo używa funkcji rozkodujA na niczaszyfrowanej wiadomości! Czynność ta, na pierwszy rzut oka dość absurdalna, ma swoje uzasadnienie praktyczne: na wiadomości W jest odciskany niepowtarzalny podpis cyfrowy nadawcy A, co w wielu systemach (np. bankowych) ma znaczenie wręcz strategiczne! Następnie, podpisana wiadomość {IV1) jest szy frowana przez powszechnie znaną procedurę szyfrującą kodujAB i dopiero w tym momencie wysyłana do B.

Odbiorca B otrzymuje zakodowaną sekwencję kodową i używa swojej prywatnej funkcji rozkodujB. która jest tak skonstruowana, że na wyjściu odtworzy podpisaną wiadomość WI. Podobnie specjalna musi być funkcja kodujAB, która z cyfrowo podpisanej wiadomości W1 powinna odtworzyć oryginalny komunikat IV.

Wymogi bezpieczeństwa zakładają praktyczną niemożność odtworzenia tajnych procedur rozkodowujących, na podstawie jawnych procedur kodujących_

Idea jest zatem urzekająca, pod warunkiem wszakże, dysponowania trzema tajemniczymi procedurami, które na dodatek są powiązane ze sobą dość ostrymi wymaganiami! Dopiero po roku od pojawienia się idei systemu z kluczem publicznym powstała pierwsza (i jak do tej pory najlepsza) realizacja praktyczna: system kryptograficzny RSA. System ten zakłada, że odbiorca B wybiera losowo trzy bardzo duże