ALG06

306

Rozdział 13. Kodowanie i kompresja danych

tekst zająłby 3x60=180 bitów. Popatrzmy teraz, jaki będzie efekt zastosowania algorytmu Huffntana w celu otrzymania optymalnego kodu binarnego.

Postępując według reguł zacytowanych w powyższym algorytmie, otrzymamy następujące redukcje (patrz rysunek 13 - 5).

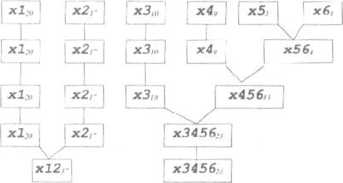
Rys. 13 - 5.

Konstrukcja kodu Huffntana - faza redukcji.

Rysunek przedstawia 6 etapów redukcji kodowanego alfabetu (Proszę nie sugerować się postacią rysunku, to jeszcze nie jest drzewo binarne!). Znaki i ,v_b występują najrzadziej, zatem redukujemy je do zastępczego znaku, który oznaczymy jako a>,. Podobnie czynimy w każdym kolejnym etapie, aż dochodzimy do momentu, w którym zostają nam tylko dwa znaki alfabetu (zastępcze). Faza redukcji została zakończona i możemy przejść do fazy konstrukcji kodu. Popatrzmy w tym celu na rysunek 13 - 6.

Rysunek przedstawia 6 etapów redukcji kodowanego alfabetu (Proszę nie sugerować się postacią rysunku, to jeszcze nie jest drzewo binarne!).

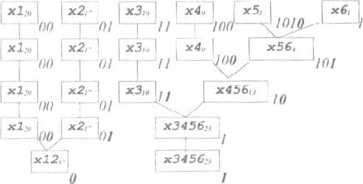
Rys. 13 - 6.

Konstrukcja kodu H uff liana -Jazu tworzenia kodu.

5)

4)

3)

2)

D

Oli

Znaki i ,v₍₎ występują najrzadziej, zatem redukujemy je do zastępczego znaku, który oznaczymy jako Podobnie czynimy w każdym kolejnym etapie, aż dochodzimy do momentu, w którym zostają nam tylko dwa znaki alfabetu (zastępcze). Faza redukcji została zakończona i możemy przejść do fazy konstrukcji kodu. Popatrzmy w tym celu na rysunek 13 - 6.