ALG03

13.2. Kompresja danych metodą Huflinana 303

Dwa krótkie sygnały oznaczają znak krótki i długi oznaczają^ itd., zgodnie z przedstawioną wyżej tabelką (0 - sygnał długi, /- krótki). Jest godne docenienia, iż marny przed sobą niewątpliwie kod... binarny! (Nawet, jeśli ów tajemniczy lud nie zdaje sobie z tego sprawy).

Załóżmy, że pewnego dnia odebrano następujący sygnał: 01II10000001 (nadawca wysłał wiadomość:    czyli „doślijcic świeże melony”). Czy

możliwe jest nieprawidłowe odtworzenie wiadomości, tzn. ewentualne pomylenie jednego znaku z innym? Spróbujmy:

0	— znakiem może być: # lub ^ lub ■»>.
01	-już wiemy, że jest to
0+ 1	- znakiem może być: ^ lub
0+ 11	-już wiemy, że jest to “*■!
<W-++ 1	- znakiem może być: "? lub
(itd.)

Pomyłki są, jak to wyraźnie widać, niemożliwe, gdyż żaden znak kodowy nie jest przedrostkiem (prefiksem) innego znaku kodowego Dotarliśmy do istotnej cechy kodu: ma on byt jednoznaczny, tzn. nie może być wątpliwości czy dana sekwencja należy do znaku X, czy też może do znaku Y.

Konstrukcja kodu o powyższej własności jest dość łatwa, w przypadku reprezentacji alfabetu w postaci tzw. drzewa kodowego. Dla naszego przykładu wygląda ono tak, jak na rysunku 13 - 3.

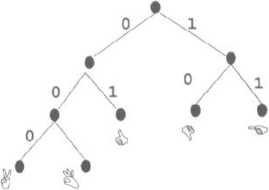
Rys. 13 - 3.

Przykład drzewa kodowego (!).

Przechadzając się po drzewie (poczynając od jego korzenia aż do liści), odwiedzamy gałęzie oznaczone etykietami 0 („lewe”) lub I („prawe”). Po dotarciu do danego listka, ścieżka, po której szliśmy jest jego binarnym słowem kodowym. Zasadniczym problemem drzew kodowych jest ich... nadmiar. Dla danego alfabetu można skonstruować ealy las drzew kodowych, o czym świadczy przykład rysunku 13-4.