CCI20130126008

AAocLęJ. oy^>^z    'wcec^. z^AJ+oLu

~Z ^J/iwlit£AA4. faieblćL

30UIV

<V^Vte^ _l.

—? Q<e>i+.

'/£- 3Ą£

^Z/n&wuA

]yi*AUr*.

jOokW

(Źr#)tUt4Co-

M

1

£7kW

U/ i^UjyCyoh    c/r<

Cxj 'y-trz /łTt07We<' eAc/d-r^jtyzs-AJ~ J*usz/^3ń. AAG.(ć>'TrstAA.'3

?'-ÓUW

JL

funn

■«^i

•v^-€

(2lc ^!aJa^ łe

r V**

'A/tp~u6wAol<

'o8>

Ay^o^Xy\r^JiA\JL (aJć*Q.Avh4j

C<{j[tA^-

^«7-50K

| 63>VVZ

L^óUykoku

fA/T&Z- Ł-tP ^/VtóC    ^£t'Vt'0>.

^ę/3    l-ją. z

2~tis3~oycArGsA^ s

o *> (*'1/hJ    kJiX

C<Cjl/l/nC^D ęJdc^^PCt^U&YTA* g r^b*S/lteC*r\

1^0? xT~(i3k "M-C*. Ary ,iA> rz^syb-c' ^/V<^*'¹

•V— Pt?2A<-^

<Ł^» C£sU.csh.

li

•r

i I

ii

1 i

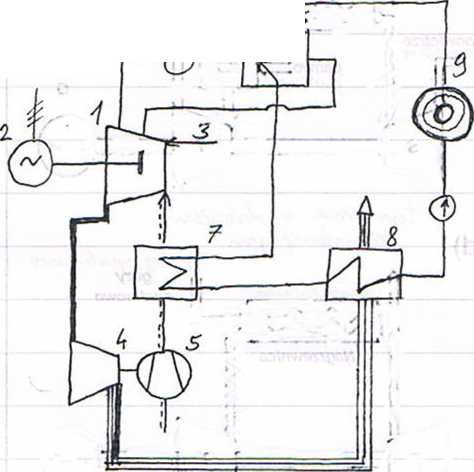
^/i~ 'ytM_/\ 'Jt( r>fłhUi/wv-<£ ■ 2 — y&. iCudrr^

3 - J-oywnp^retjJrtiAcić    j 3-~ T-lAf>2ri™.h2

-uA/i*-J*-C Jjo^oyU^Ące.^0 '_f S~~ 'łfrr-ęfżasdlt<. yLOWtArZn. j ^ ~ (JiĄ/(c<I‘\AA-+- olzjU 2o 'YWU, ■ 'y~V'ir&s^<#^ '>fbtłJi& ’_f 7 ~~ <J/otJiMt&. ywv.j 8 ~ cAit ccWaoa ojI&IpW j 3 ^— cAlnOvt^ ćj-fjllA-