geomechana3

-48-

-48-

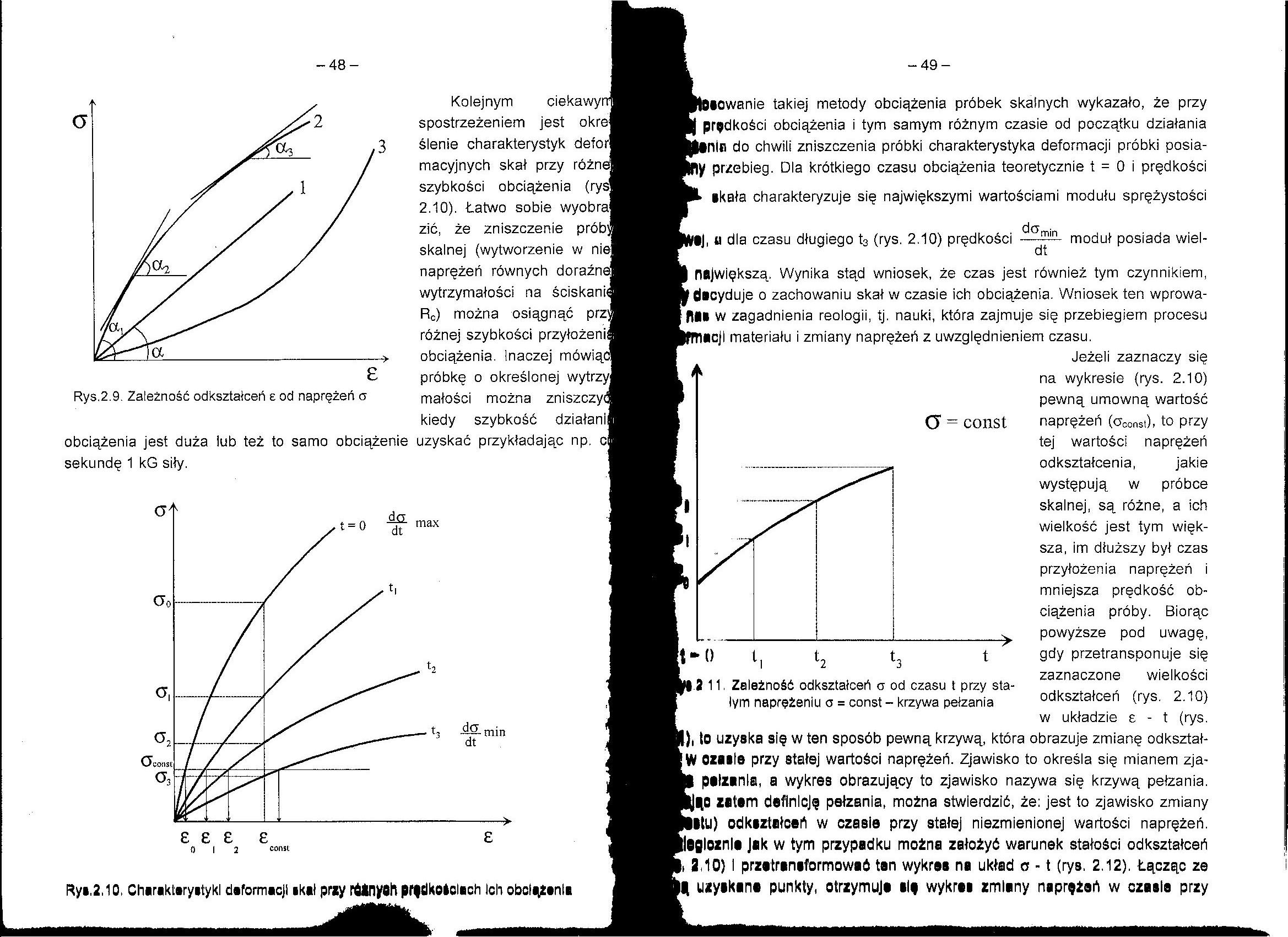
Rys.2.9. Zależność odkształceń e od naprężeń a

obciążenia jest duża iub też to samo obciążenie sekundę 1 kG siły.

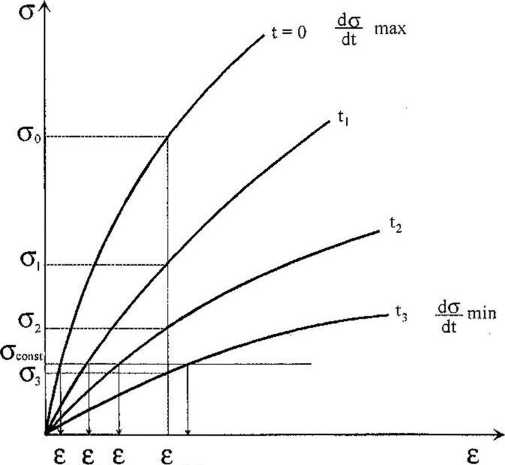
Kolejnym ciekawyrr spostrzeżeniem jest okre sienie charakterystyk defor macyjnych skał przy różne' szybkości obciążenia (ryś 2.10). Łatwo sobie wyobra zić, że zniszczenie prób} skalnej (wytworzenie w nie naprężeń równych doraźne wytrzymałości na ściskani* R_c) można osiągnąć prz) różnej szybkości przyłożeni! obciążenia. Inaczej mówiąc próbkę o określonej wytrzy małości można zniszczy*! kiedy szybkość działanii uzyskać przykładając np. ci

0    |    2 const

Ryt,2,10, Churnktiryitykl diformicji ikil przy rttnyoh pf|d kolei ich ich obclą?»nli

iowanie takiej metody obciążenia próbek skalnych wykazało, że przy prędkości obciążenia i tym samym różnym czasie od początku działania nlfi do chwili zniszczenia próbki charakterystyka deformacji próbki posia-y przebieg. Dla krótkiego czasu obciążenia teoretycznie t = 0 i prędkości

łkała charakteryzuje się największymi wartościami modułu sprężystości

•j, u dla czasu długiego t₃ (rys. 2.10) prędkości ^damin moduł posiada wiel-

dt

największą. Wynika stąd wniosek, że czas jest również tym czynnikiem, decyduje o zachowaniu skał w czasie ich obciążenia. Wniosek ten wprowa-flil W zagadnienia reologii, tj. nauki, która zajmuje się przebiegiem procesu ■cjl materiału i zmiany naprężeń z uwzględnieniem czasu.

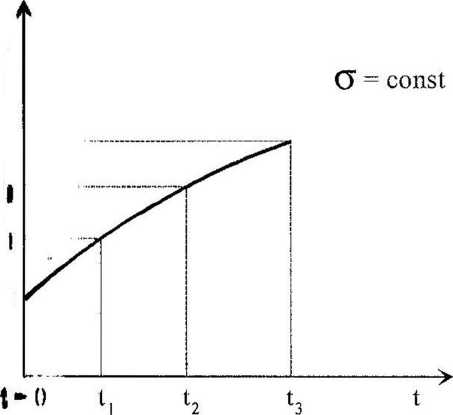
211. Zależność odkształceń o od czasu t przy stałym naprężeniu o = const - krzywa pełzania

Jeżeli zaznaczy się na wykresie (rys. 2.10) pewną umowną wartość naprężeń (a_const), to przy tej wartości naprężeń odkształcenia, jakie występują w próbce skalnej, są różne, a ich wielkość jest tym większa, im dłuższy był czas przyłożenia naprężeń i mniejsza prędkość obciążenia próby. Biorąc powyższe pod uwagę, gdy przetransponuje się zaznaczone wielkości odkształceń (rys. 2.10) w układzie e - t (rys. ), to uzyska się w ten sposób pewną krzywą, która obrazuje zmianę odkształ-W OZBils przy stałej wartości naprężeń. Zjawisko to określa się mianem zja-pełzenla, a wykres obrazujący to zjawisko nazywa się krzywą pełzania, ąo zetem definicję pełzania, można stwierdzić, że: jest to zjawisko zmiany Itu) odkeztałceń w czasie przy stałej niezmienionej wartości naprężeń. l6Qloznle jik w tym przypadku można założyć warunek stałości odkształceń ₍ 2,10) l przetreniformoweć ten wykres ne układ o -1 (rys, 2.12). Łącząc ze l uzyikene punkty, otrzymuje elf wykree zmleny naprężeń w czasie przy