IMAGE0140

130

T = -EJ^—y- - P -» T_l = -EJv7 =    + 2v, - 2v₅ + v₆) = P —>

dx-    ^L 2X^}    '

⁸ EJ

Wektor ugiąć węzłowych V ma postać

V = { 1.0C 0.0 1.0C 3.5C 7.0CI1.0C 15.0C 18.5C }.

Uzyskane rozwiązanie MRS przy obciążeniu siłą skupioną, uwzględnianą w warunku brzegowym sprzężonym z trzecią pochodną podstawowej funkcji (funkcji ugięcia), jest obarczone znacznym błędem, co wynika z porównania wartości ugięcia swobodnego końca, wyznaczonego analitycznie i z użyciem MRS

PI³

v^ilnal1' (L) = 0.333——- ,

EJ

v^MRS (L) = v₄ = 11.0 • —- = 11.0 •    • f-1 = 0.344— = 1.03 ■ v^an;llit (L).

⁴    EJ    EJ UJ    EJ

6.5. Zastosowanie MRS do rozwiązania zginanej płyty (U)

W ramach mechaniki ustrojów powierzchniowych należy obowiązkowo zaznajomić się z równaniem przemieszczeniowym prostokątnej płyty zginanej.

opisanej w kartezjańskim układzie współrzędnych. Jest to równanie różniczkowe czwartego rzędu o pochodnych cząstkowych

V²V²w(x,y)) = p_(x,y)l D.    (6.12)

Niewiadomą w tym równaniu jest funkcja ugięcia płyty w(x,y), wywołana obciążeniem poprzecznym p_z(x,y). Sztywność płyty jest scharakteryzowana stałą

12(1 - v²)

w której występuje obok modułu Younga E - współczynnik Poissona v oraz grubość płyty h .

Znając rozkład funkcji ugięcia w(.t,v) możemy wyznaczyć w dowolnym punkcie płyty momenty zginające m_x(x,y) i m_y(x,y) oraz momenty skręcające m_AV(x,v), korzystając z następujących związków, wynikających z połączenia związków fizycznych i kinematycznych obowiązujących dla płyty zginanej:

d^:vv d²w = --^D(-r-r + v_T—), ćx “    ćy~

(6.13)

^ 3“w d"vv

'»,■ ^=_D(T^{_r + v}T^⁾’

ery" dr"

d w dxdy

W!„. = -D(l-v)

W dalszym ciągu zbudujemy przybliżone rozwiązanie z zastosowaniem MRS dla płyty kwadratowej przegubowo podpartej, z obciążeniem równomiernym p_z(x,y) - p - const.

W przypadku ustroju powierzchniowego mamy do czynienia z dwuwymiarowym obszarem. Punkty węzłowe w MRS otrzymamy w wyniku przecięć dwu rodzin linii równoległych do osi x i y , przyjmując stały krok siatki różnicowej X-Ax = Ay.

Na rysunku wprowadziliśmy dwa warianty siatki różnicowej, przyjmując krok siatki X = U4 lub X = U8.

Równanie różniczkowe zginanej płyty (6.12) zawiera po jego lewej stronie operator bilaplasjanu, którego szczegółową postać zapiszemy poniżej

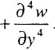
(6.14)

2v7 - ,    , W d⁴W

V V w{x, y) = -—— + 2—-—-dx dx²dy²

Zgodnie z ideą MRS zastąpimy go odpowiednim operatorem różnicowym, budując równanie różnicowe, które będzie zapisywane dla kolejnych węzłów siatki różnicowej, z oznaczeniem bieżącego punktu centralnego za pomocą indeksów i,k oraz zmianą indeksu i przy uwzględnianiu kroku siatki A.v , a także indeksu k odpowiednio w kierunku osi y

V-V^|„, = -{2°w_a -8(w,.__u +w_j+u +w_iMl+w_ik__{) +

(6.15)

⁺ 2(W,+ Wj., _<+, + VV-_f+u_, + W,_fU+1 ) +

-2.lt + ^wi+2.k + ^W,.k ₊ 2 + ^WU-2)1 ^:

Pi,*

O

Powyższe równanie można przedstawić w postaci graficznej (rys.6.5), przypisując węzłom siatki różnicowej współczynniki, przez które należy pomnożyć ugięcia w kolejnych punktach. Jak widać na rysunku zasięg schematu różnicowego wynosi 4A, w obu kierunkach.