img075

244 V. Metoda reprezentacyjna

tego parametru pozostaje statystyka m'a_t tj. częstość występowania elementów wyróżnionych w próbie, ale estymator len w przypadku losowania zależnego ma rozkład hipergeoinetryczny. Wariancja estymatora min określona jest wtedy wzorem

(5.7)

W —W-~" ^pq

\n J W -J ' « ‘

gdzie A^T jest liczebnością populacji, p — ułamkiem właściwym wyrażającym = frakcję elementów wyróżnionych w populacji, a q-\-p. Korzystając^: z faktu, że statystyka m'n ma w dużej próbie rozkład asymptotycznie normalny. można zbudować przedział ufności dla wskaźnika struktury p-populacji generalnej w oparciu o rozkład normalny. Wzór na przedział' ufności dla p oraz wynikający z niego wzór na liczebność próby przy szacowaniu p z żądaną Z góry dokładnością w schemacie losowania zależnego próby podane są w poniższych modelach.

Model I. Populacja generalna ma skończona liczbę .V elementów. Badamy w tej populacji cechę niemierzalną. Spośród A elementów populacji, M jest elementów wyróżnionych, tj. mających badaną cechę jakościową. Wskaźnik struktury tej cechy, tj. frakcja elementów wyróżnionych w populacji, wynosi zatem p—M!.V(po przemnożeniu przez 100 otrzymujemy procent). Z populacji tej wylosowano przy użyciu schematu losowania zależnego dużą próbę (« co najmniej kilkaset), na podstawie której należy oszacować nieznaną frakcję p elementów wyróżnionych w populacji.

Przedział ufności dla wskaźnika struktury p (jeżeli nie jest on zbyt dużą lub zbyt małą liczbą) można Otrzymać według wzoru

(    ¹ m fl

[ m    I jV — w n y    n J

(5.8) P\----<P<

ln \ N-i    n

i    m ( rwYi

m

<---u

n

I    * V n)j

’\i iv-l »    >

We W2orze tym m jest liczbą elementów wyróżnionych znalezionych w elementowej próbie, a u_a jest wartością odczytaną z tablicy rozkładu normalnego A^T(0, I) dla założonego z góry współczynnika ufności l-ar.

Gdy populacja generalna jest duża (jV> tOOO), wtedy można przyjąć, ie 1 •(>'- l)a. 1,'Aj i wzór (5.8) na przedział ufności można zapisać najprościej w postaci

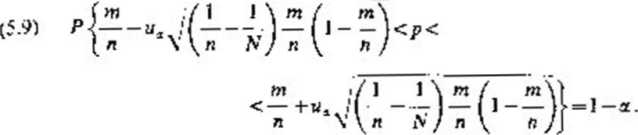
Model U. Populacja generalna ma skończoną liczbę iY elementów, w tym wyróżnionych jest M elementów mających określoną cechę niemierzalną. Frakcja p= Mp.V elementów wyróżnionych jest nieznana. Chcemy na podstawie próby wylosowanej z tej populacji przy użyciu schematu losowania zależnego oszacować frakcję p z błędem maksymalnym d. Jeżeli znany jest rząd wielkości szacowanej frakcji p, to potrzebną liczebność próby można obliczyć ze wzoru

A

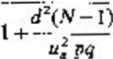
(5-10)

gdzie jV jest liczebnością populacji, p - spodziewanym rzędem wielkości szacowanej frakcji, q= 1 — p_y u* jest wartością odczytaną z tablicy rozkładu iV(0, 1) dla przyjętego współczynnika ufności J - a, a ^jest dopuszczalnym, maksymalnym błędem szacunku frakcji p i podawanym w ułamku dziesiętnym).

Jeżeli nie jest znany rząd wielkości szacowanej frakcji p_t to przyjmując za iloczyn pą jego maksymalną wartość i, utrzymujemy przybliżony wzór na liczebność próby przy szacowaniu frakcji p elementów wyróżnionych w populacji dla losowania zależnego próby:

(5-11)

N

4d²(N-\)

1 +    5    '