img026 2

Belka 1-2
	- R2 • 4 + P, • 2 = 0	stąd	R2 = 4kN
IT = o,	R]+R2 -P, =0	stąd	R{ = 4kN
Belka 3-D-E
ZM}= 0,	P2 • 4 - ■ 2 + ?2 • 2 ■	1-0	stąd /?D=8kN
M ►C II o	R3 d" R/J ~ ~~ ^Ch ' 2 ^=	0	stąd /?3=-lkN
Belka A-l
zma = o,	Ma +Ri - 4 = 0	stąd	Ma =-16kNm
1^ = 0,	RA-Rt=0	stąd	Ra =R,= 4kN

Belka 2-B-C-3

SM_r = O,    - i?₂ • 6 + M + /^ • 4 + (/, • 2 • 1 + 7?₃ • 2 = O stąd    7?_B=3kN

zr = 0,    - R₂ + R_k + Ą. - g, • 2- R₃ = O    stąd    /ć_r=2kN.

Poprawność obliczenia reakcji sprawdzono dla belki przegubowej jako całości, biorąc np. ZM_E = 0

4-20-16-8-14 +12 + 3-10 + 2-6 — 1- 25-2 -2-3+ 8-2 = 0

Siły wewnętrzne

Przykładowo obliczono siły wewnętrzne w belce 2-B-C-3.

•    przedział 2-B, 0 < x < 2m V(x) = -R₂ = -4kN = V₂=Vg

M(x) = -R₂-x = -4-x, M₂(0)=0,    M^/B(2)=-8kNm

•    przedział B-C, 2 in < x< 6m V(x) = -R₂ + R_a = -4 + 3 = -lkN

M(a) = -R₂ - * + M + (x - 2) = -4x + 12 + 3(x-2)

Mg(2)=4kNm M[(ó) = OkNm

•    przedział 3-C, 0 <    < 2m

V(x_i) = R_i+q_rx_] = -1 +1 - je,,    K₃(0)=-lkN,    P'_c^/’(2) = lkN

2    "5

M(x_]) = -R₃.x_i-^f- = \.x-^L, M₃ (o) = 0,    Mg( 2)=0

Ekstremum momentu zginającego:

K(.v,) = -1 + x, = 0 skąd =lm M_inax(x, =l) = 0,5kNin.

Wykresy sił wewnętrznych przedstawia rys. 1,54c.

u ili/nj;|c wykresy sił wewnętrznych, należy zwrócić uwagę na ciągłość wykresu V miejscu nieobciążonych przegubów wewnętrznych, jak również na zerowe U|iuii' nty zginające w tych miejscach.

jfmlinle 1.34.

■lit Mki obciążonej jak na rys.l.55a sporządzić wykresy sił przekrojowych.

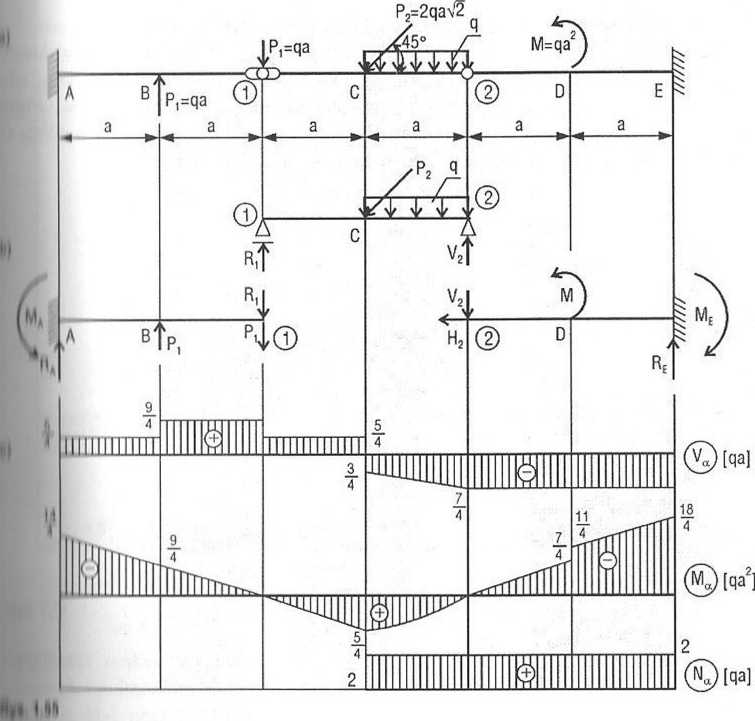
Bil i' podporowe: film I '

5 qa

*■ =

fo ²

I u    R_r2a-P₂- — -a-^- = 0

¹ 2 2 2

63