img029 2

2.4. Warunki równowagi układów sił

Warunkiem geometrycznym równowagi zbieżnego układu sił jest utworzenie przez te siły wieloboku zamkniętego.

Zbieżny układ sił pozostaje w równowadze wówczas, gdy ich wypadkowa W, a więc także rzuty jej składowych na osie x, y układu współrzędnych są równe zeru:

w_x=t P_ix = zx = o, w_y = i P_iy. = ry= o.    (2-6)

i= 1    i— 1

Oznaczenie jak we wzorze (2-2).

Warunki (2-6) oznaczają, że zbieżny układ sił jest w równowadze, gdy sumy algebraiczne rzutów wszystkich sił układu, odpowiednio na oś x i y, są równe zeru.

Dowolny płaski układ sił pozostaje w równowadze, gdy zamykają się jednocześnie: wielobok sił i wielobok sznurowy. Są to tzw. wykreślne warunki równowagi płaskich układów sił niezbieżnych.

Analityczne warunki równowagi dowolnego płaskiego układu sił są następujące:

1)    suma algebraiczna rzutów wszystkich sił na oś x równa się zeru

t ^pu =    =    (2-7)

i = 1

2)    suma algebraiczna rzutów wszystkich sił na oś y równa się zeru

t Piy = £y= 0,    (2-8)

i = 1

3)    suma algebraiczna momentów statycznych wszystkich sił względem dowolnego punktu leżącego na płaszczyźnie działania sił równa się zeru

t ^pi^ri =    = 0.    (2-9)

i= 1

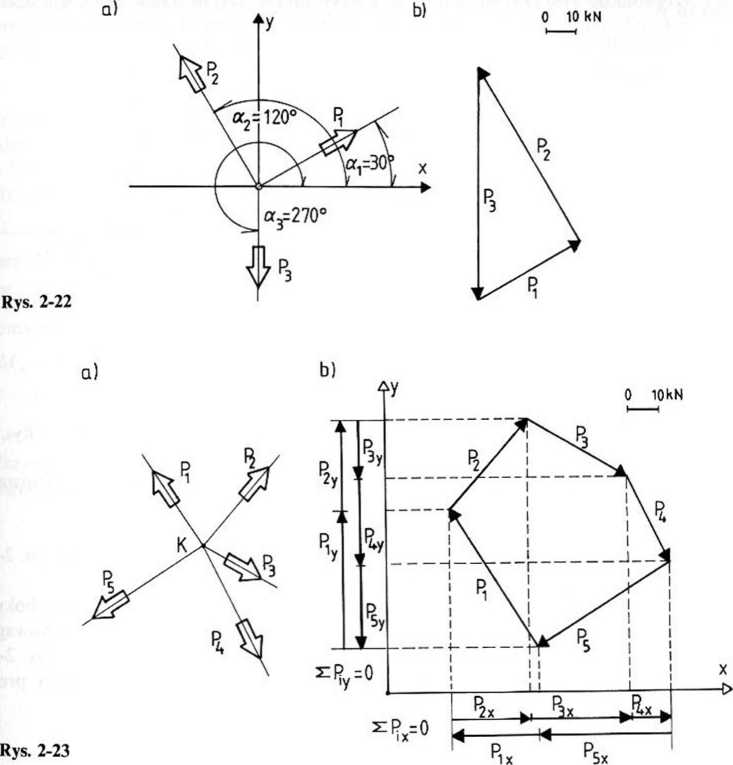
Przykład 2-15. Sprawdzić wykreślnie równowagę układu trzech sił, przedstawionego na rys. 2-22a. Dane: P, = 40 kN, P₂ = 70 kN, P₃ = 80 kN.

Warunkiem koniecznym, aby trzy siły nierównoległe mogły być w równowadze jest przecinanie się tych sił w jednym punkcie oraz zamykanie się odpowiadającego im wieloboku (trójkąta) sił. Jest to tzw. twierdzenie o równowadze trzech sił. Zbieżny układ trzech sił przedstawiony na rys. 2-22a będzie w równowadze, gdy wielobok tych sił będzie zamknięty. W wypadku danych sił zbudowany wielobok jest zamknięty (rys. 2-22b), a więc układ sił jest w równowadze.

Przykład 2-16. Przedstawić graficznie równowagę zbieżnego układu sił, pokazanego na rys. 2-23a. Dane: P, = 55 kN, P₂ = 40 kN, P₃ = 38,5 kN, P₄ = 32,5 kN, P₅ = 52,5 kN. Rozwiązanie pokazano na rys. 2-23b.

W celu zilustrowania związku między wykreślnymi i analitycznymi warunkami równowagi, przyjęto układ współrzędnych x, y jak na rys. 2-23b oraz zrzutowano wykreślnie składowe P_ix i P_iy na osie tego układu. Otrzymano: ZP_ix = 0 i IP,_y = 0. Oznacza to, że zamknięcie się wieloboku sił jest równoznaczne ze spełnieniem się analitycznych warunków równowagi (2-6).

Przykład 2-77. Sprawdzić analitycznie równowagę układu czterech sił pokazanych na rys. 2-24. Dane: P, = 40 kN, a, = 0°, P₂ = 30 kN, a₂ = 60°, P₃ = 39,05 kN, a₃ = 90°, ^4 = 78,26 kN, a₄ = 225°.

Rzuty sił P_;:

- na oś x:

P_lx = PjCosO" = 40,0 kN,

P_2x = P₂cos60° = 15,0 kN,

P_ix = P₃cos90° = 0,

P_4x = P₄cos(180° + 45“) = -55,0 kN,

AT.