KONSTRUKCJE STALOWE STR064

64

r

•    w obliczeniach statycznych uwzględniono jedynie imperfekcje globalne (przechyły) oraz efekty P-A (przesuw węzłów). Należy sprawdzić stateczność każdego pręta przy zastosowaniu formuł interakcyjnych (6.61) i (6.62) normy [51] (patrz pkt 7.3), przyjmując długość wy-boczeniową słupów jak dla ram o węzłach nieprzesuwnych. Norma [51] zezwala, aby długość wyboczeniową słupów przyjmować wtedy równą ich długości teoretycznej (wysokości słupa),

•    w przypadkach gdy spełnione jest kryterium z procedury 4.4, obliczenia statyczne można wykonywać według teorii I rzędu z pominięciem imperfekcji. Stateczność prętów należy wtedy sprawdzać według interakcyjnych formuł wyboczeniowych, przy czym długość wy-boczeniowa słupów powinna odpowiadać globalnej postaci wyboczenia układu konstrukcyjnego (jak dla ram o węzłach przesuwnych) oraz uwzględniać wpływ sztywności elementów i węzłów, istnienie przegubów plastycznych oraz rozkład sił ściskających.

Przykład 4.11

Ocena wrażliwości ramy na efekty II rzędu oraz wyznaczenie

sił fikcyjnych

T

Odniesienie w normie

~2

Odniesienie w skrypcie

Korzystając z danych z przykładu 4.10, zbadać, czy rama jest wrażliwa na efekty II rzędu oraz wyznaczyć siły fikcyjne.

Rama jest niewrażliwa na efekty II rzędu, gdy spełniony jest warunek:

cc„ > 10.

‘cr

W odniesieniu do ram regularnych można stosować:

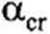
	f h ]
^ ^VEd ,	^^5H,Ed,

>10

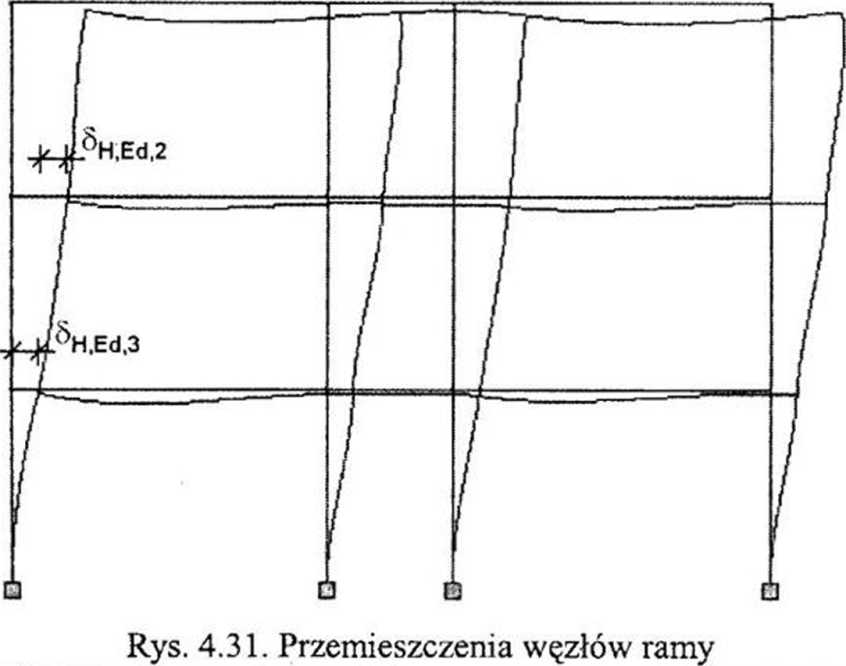
Wartości względnych przesuwów węzłów 5h,e<i (rys. 4.31) wyznaczono programem ROBOT od obciążeń obliczeniowych oraz sił od imperfekcji globalnych, stosując schemat statyczny i obciążenia jak w przykładzie 4.10 (rys. 4.24 i 4.26).

4^^H’^Ed'¹

procedura

4.4

\\

i

i

r

wzór (5.1) normy [51]

wzór (5.2) normy [51]

wzór (4.14)

wzór (4.16)

{

|

i

i

»

I

i

i

i

r

ł

f

I

t

y