mech2 3

4

1	2	3
13	5 coa Ą- t2	—5 sin y- t^2
.14—	-2t - 2	2 ~ t + 1
15	4 OOS -y t	-3 sin -g- t
16	3t	4t^2 + 1
17	7 sin^2 -g- t - 5	— 7 oos^2 -g- t
18	1+3 003 -y t^2	3 sin | t^2 + .3
19	-5t^2 - 4	3t
20	2 - 3t - 6t^2	3 —|* t - 3t^2
21	6 sin -g~ t^2 — 2	6 cos -g- t^2 + 3
22	7t^2 - 3	5t
23	3 - 3t^2 + t	4 - 5t^2 + Ą- t
24	-4 oos -5- t - 1 3	—4 Bin g- t
23	-6t	-2t^2 - 4
26	„ 2 ^n8 cos -g- t + 2	-8 sin^2 -g- t - 7
27	-3-9 sin -g- t^2	-9 cos -g- t^2 + 5
28	-4t^2 + 1	-3t
29	5t^2+ t -3	3t^2 + t + 3
JO	2 cos -y t^2 — 2	-2 sin -y t^2 + 3

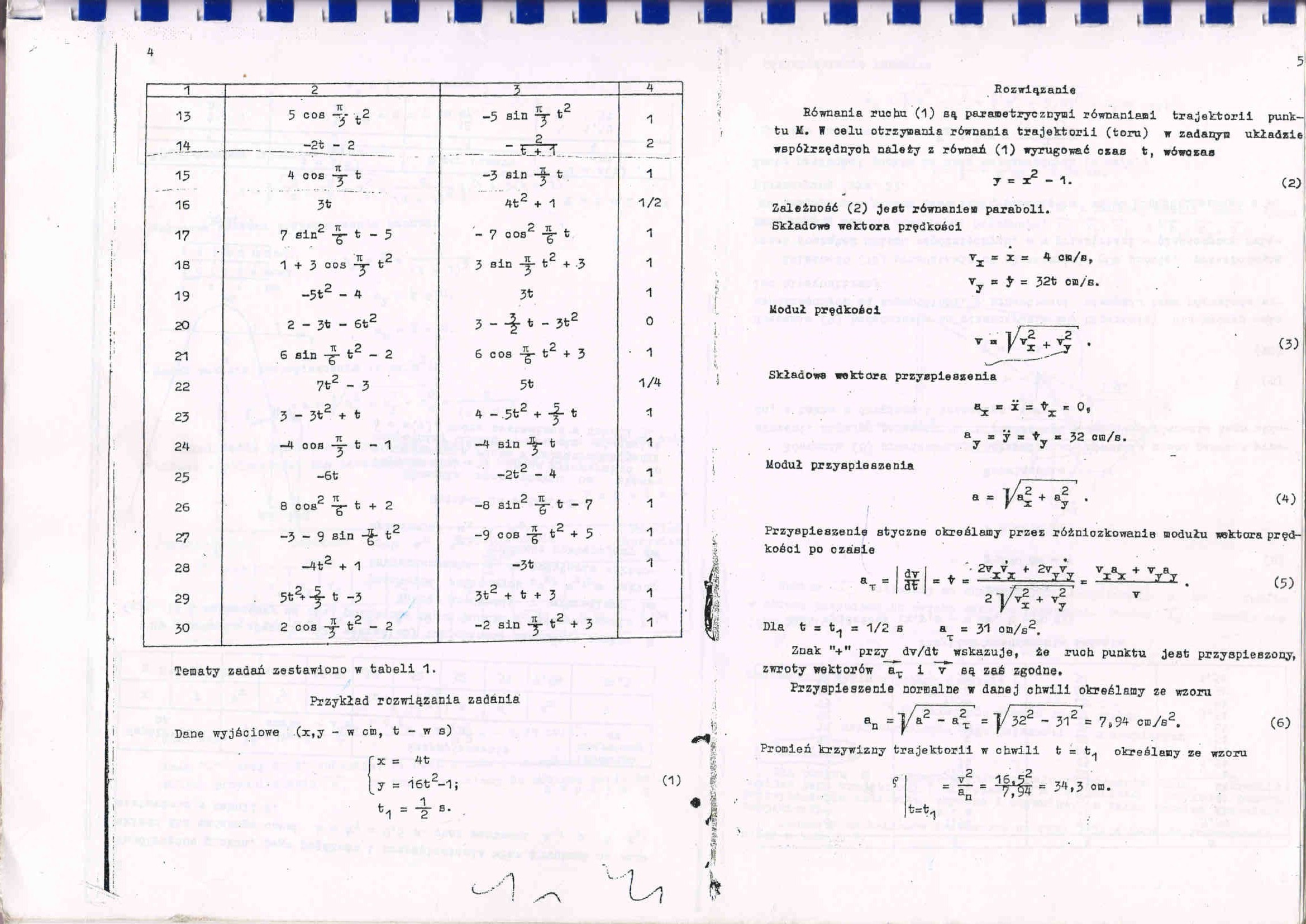
Tematy zadań zestawiono w tabeli 1.

Przykład rozwiązania zadania Dane wyjściowe (x,y - w cin, t - w s)

r x = 4t

[7 = “let²-^

1

2

1

1/2

1

1

1

0

1

1/4

1

1

1

1

1

1

1

1

Rozwiązanie

Równania ruohn (1) są parane trycznyrai równaniami trajektorii punktu M. W oelu otrzymania równania trajektorii (toru) w zadanym układzie wepółrzędnyoh należy z równań (1) wyrugować czas t, wówczas

y = X² - 1.

Zależność (2) jest równaniem paraboli. Składowa wektora prędkości

T_x a I a 4 C»/B, V_? a J = J2t om/B.

(2)

Moduł prędkośoi

(3)

Składowa wektora przyspieszenia

Moduł przyspieszenia

0,

a a y =e s J2 ora /a. 7    7

r

Przyspieszenie styczne określamy przez różniozkowanie modułu wektora prędkości po czasie

_ dv ^ar = 3F

(5)

-r

Dla t = t. = 1/2 s a = 31 om/s².

'    T

Znak "+" przy dv/dt wskazuje, że ruoh punktu jest przyspieszony, zwroty wektorów a_T i r są zaś zgodne.

Przyspieszenie normalne w daDej chwili określamy ze wzoru

^an = y^&2 “ ^a r = ]/32² - 31² = 7*94 cra/s².    (6)

Promień krzywizny trajektorii w chwili t = t^ określany ze wzoru

+ v_

CD f^!

t=t.

L

1

i