mech2 88

174

Stąd noaent względem średniej

^ - i"s²+ j *^uZ-

Zadanie 10

Wyznaczyć moment bezwładności prostego Jednorodnego stożka kołowego o nasię M, wjBokośoi b. i średnicy podstawy 2E względem a) osi stożka, b). średniay podstawy.

Bozwiązanie

a) monent bezwładności stożka względem osi z wyznaozymy znająo moment bezwładności elementarnej masy będącej waloem o wjBokośoi dz i promieniu podstawy r(z)

dl.

dn * r

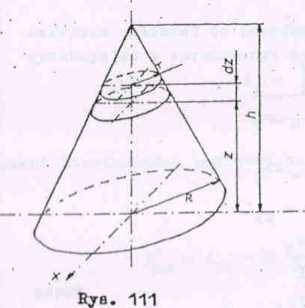
dm *r y n r da, H

Y* B

«' - _h-

b

^dI— ■    Tf (b - *)⁴ da,

ynH⁴ ,5    Yufi⁴h

zr ^b

5*2h^{4    10}

M b y j rtH²b,

^T - ^ ^mZ>

zz

dz

b) moment bezwładności względem średnioy wyznaozymy Jako sumę momentów bezwładności względem płaszazyzn 1 do osi y i z

*xr - ^Jz ⁺ V

1

fiŃB    ■■■—n "i ■

175

Wyznaozamy I

z² da,

do a V ⁿr dz, H

h

= E (t - z),

i_z = J y nz² ^ (h - a)² Az «= -*-^f J z² (h - z)² de

h

YtiS² 7 #2.2 „ 5_h . _^K - Y nR² f1 _3^2 = "■* 2” J    U a -2z b + z J dj o -l    za —

-₂.    -^0_b⁵-l *⁵-*»⁵>

I_ ₌ JL**! _h5 , XS|^2 „ ^ m_Ł2.

30h^c

icr

Wyznaczamy T^. = 1^.

^[zz =    V

Ostatecznie moment bezwładności względem średnioy

MR

2.1

TO

Mh^£

² « gy (3E² + 2h²) .

Zadanie 11

Wyznaozyć moment bezwładnośoi stożka z poprzedniego zadania względem prostej przeahodząoaj przez wierzchołek równoległej do średnioy podstawy.

Odp. I =    M(4h² + H²).

Zadanie 12 (rys. 112)

Wyznaozyć moment bezwładności olała złożonego ze stożka kołowego o maaie^M-i i wysokości h oraz półkuli o masie M₂ i promieniu podstawy fi względem osi prostopadłej w wierzchołku do osi stożka.

Odp

. I_L = M₁ ^_źq    + M₂ (f B² + f Eh + h²).