s25 z 2 3 4

0

* y ł> «,vA ■

' .

•' i<K.C l 3 • i dj

» i ł ? ? ON . 5 H p vi* j Cc. [(.rj.cj

Repetytorium z matematyki dla logistyków

V*¹ • -,c*

Podobnie jak dla rachunku zdań i kwantyfikatorów podamy ważniejsze prawa algebry zbiorów:

prawa przemicnności:    AuB=BuA

AnR=Rn A

prawa łączności:

prawa rozdzielności:

prawa de Morgana:

Au(BoC)= (AuB)uC A n (BnC)=(AnB)nC Au(BnC)=(AuB)n(AuC) A n (BuC) = (A n B)u (a n C) (A aB) = A'uB'

(AuB) = A'nB'

prawa tautologii:    A vj A = A, A n A = A

A u 0 = A, Aa0 = 0 A u U = U, AnU = A.

Posługując się tautologiami rachunku zdań i definicjami działań na zbiorach, sprawdzimy jedno z praw rozdzielczości:

Aa(RuC) = (AaB)u(AaC)

X £ L «=> XG [An(BuC)]»X6 Aax€ (BuC)« »X£Aa(x6Bvx6C)«(x6AaXS B)v(x€ AaX€C)»

<->xe (an B)vxe (AnC)«x€ [(AAB)u(AnC)|o xe P.

Zadania

I. Obliczyć AuB.AnB, A\B, B\Adla następujących zbiorów:

B= {c.d|

B = {a.b.d}

B = {(a. b}. a. {b}}

a) A = {a, b, c.d},

b)    A={a. h, {c}}.

c)    A = {{a, {b}).c, (a, b}},

1 w
-2>< 3		\ > 1»>3 łi
	i 3-»<3
'/ >-c		^ s }/:
»<c	> 'O	V 'A , n.t V M*
^v\\	1 n—!

J.

o ;    5

>e < i

Dla zbiorów:    a) fi a ó

A = (x: |3 - x|<3)

B = {x:|2x+ 1|> 2

C = |x:i_£|x

D =

X I j—r > X* - X + X

E =

x:———£2

x-l

d) ^y &
9 : fy>l<3 '$<$•*< 3	O: i _ł'* ’
3 -x < 3 3->*-3	ix<5
'X <o -x >-C	3 v .

-cc

F = /x : log, (x^! — s)> 0|

&

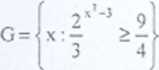
k ^Z./i > O („-* ) fx i., 1+0

O    G

f): * £ (0,6) S':K f- ic,o

obliczyć:

a)    A n B

b)    C\D

c)    EuF

d)    A’ u G

~A O    A C

v5ł : V £•{- *9, '/> ^/,1,

3.    W następującym układzie współrzędnych zaznaczyć zbiory A, R,

AnB, AuB:

a)    A={(x, y):    xy>0}

B = {(x.y): sin (x + y) = 0}

b)    A = {(x, y): cos(x-y) = 0}

B = {(x. y): ctg y = 0}

4.    Udowodnij, że dla zbiorów zachodzą następujące równości:

a)    A\(BuC) = (A\B)n(A\C)

b)    A\(BnC) = (A\B)u(A\C)

c)    A n (A \ B) = A \ (A o B)

d)    (A\B)uB = A’j B

e)    A\B=(AuB)\B

0    (A\B)n(C\D) = (AnC)\(Bu D)

(y °-l * ^e L'^:> x<£ jjmól ‘•C c Ą a x t ($„c )*■> >*•<»,• _A e f*3 >e lOi ■>    a > ₄ V_;/. e c'ko

Odpowiedzi    i.t,« *._£c‘y*>^» ^

- -S l./Wę (ii \c v-' -la) AuB = {a, b. c,d] '    *

AnB = {c,d)    ■«***£*

A \ B = {a b I    —:C')^

' '    V . < S - ^ > £ C    -i ‘i •    Vo

B \ A = 0    <0    .5 j ■, \ £ ('a \ c Iro , • =

Ib) A u B = {a. b, d, {c}} c)xv l    x > e p a * e(rt'tyo

An B = (a, b}    * (^x * ^p ** /<?)*> >

A \ B = {(c}}    x<* a    3ki> i»\ j

B \ A = (d}    a) x £ic*> £(<»v<ł! •/    (**a _ft )_v „*