skanowanie0062

Fizyka Sem. I,

INFORMATYKA,

TEST PRZYKŁADOWY KT2

Odpowiedz na poniższe pytania. Odpowiedzi zaznacz na arkuszu, który otrzymałeś z tym zestawem. Na każde pytanie jest tylko jedna dobra odpowiedź. Odpowiedź zaznacz znakiem X. Jeśli się pomyliłeś X obejmij kółkiem .

•    Wpisz na arkusz odpowiedzi numer otrzymanego testu .

•    Na arkuszu pytań testowych nie wolno robić żadnych notatek, znaków zaznaczeń. Życzę powodzenia!

1. Konfigurację elektronową elektronów w niewzbudzonym atomie sodu (Na o liczbie atomowej Z=ll i masowej A=23) możemy zapisać:

A) (ls)²(2s)²(2p)⁴(3s)² (3p)‘,

B) (1 s)^l(2s)^I(2p)²(3s)^l(3p)²(3d)⁴, D) (1 s)²(2s)²(2p)¹(3s)²(3p)¹(3d)²

2. Jeżeli drganie harmoniczne jest opisane równaniem: A[t) - A_n cos(ó)x + (p ₀) to przyspieszenie a w tym ruchu harmonicznym możemy wyrazić zależnością:

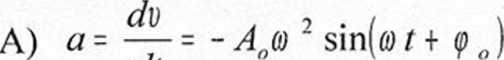
dl

dx

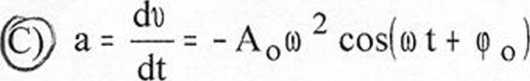
B) a = — = A_o(0 ² cos(ó) t + ę ₀

dt

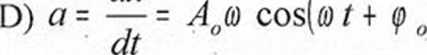
gdzie: A_u - amplituda drgań, co - częstość drgań, t - czas, <p₀ - faza początkowa drgań.

3. Iloczyn wektorowy dwóch wektorów a i b (oznaczamy symbolicznie a x b) jest:

A) skalarem, którego wartość liczbowa wyraża się iloczynem wartości liczbowych danych wektorów przez cosinus kąta a zawartego między nimi,    czyli: a • b = ab cos a

B) nowym wektorem Ć : a x b = c o wartości liczbowej c: c = ab sin a , (gdzie a jest kątem utworzonym przez kierunki wektorów a i b), i kierunku wektora a (mnożnej),

C) skalarem c, którego wartość liczbowa wyraża się iloczynem wartości liczbowych danych

wektorów przez sinus kąta a zawartego między nimi, czyli: c = ab sin a ,

kątem utworzonym przez kierunki wektorów a i b), kierunku prostopadłym do płaszczyzny wyznaczonej przez wektory a i b, i zwrocie określonym regułą śruby prawoskrętnej.

4. W cieczach i ciałach amorficznych (np. szkle) występuje:

A)    jednakowe radialne uporządkowanie (atomów jonów lub cząsteczek) we wszystkich kierunkach,

B)    pewne okresowe uporządkowanie cząsteczek dalekiego zasięgu w całej przestrzeni,

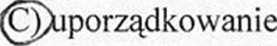bliskiego zasięgu,

D) uporządkowanie tylko wewnątrz pewnych obszarów zwanych krystalitami.

1

czasu) dla cząstki o masie m w polu siłowym o potencjale U(x) ma postać:

2

Stacjonarne, jednowymiarowe równanie Schródingera (tzw. równanie Schrodingera bez