skanuj0049 3

( I)^{1 1} iiiii 2u, i

Yn K ^aoi) “ P 10,5 (£(-1)' ¹ a, + 8_fcla_al) + 0,25(£(

i = 1    i-l

fcl

+ 8_fcl sin 2aJ] - cos a (£(-l)'^_1 sin a, + 8_fcl sin aj,

i=i

m    m

Y₆ (a, aj = P [0,5( £(-l)^M a,. + 5^ aj + 0,25 ( £(-l)^i_1 sin 2a_f +

k2+\    k2 + l

m

+ 8_fc2 sin 2aJ] - cos a ( ^(-lp¹ sin a,- + 8_fc2 sin aj,

fc2 + l l

Y₇ (a,J = £(-l)‘~¹ sin a,- + 8,sin a_b,    (7.42)

i=i

/cl

y« (^aai)=X(~^1)1-1 sin a< ^{+ sin a}°l’

1=1

m

Y'j (“J = K-r^{1 sin a}, ⁺ 5k2 ^{sin a}«2-

fc 2 + 1

7.5. Przekroje o złożonych kształtach

Elementy o złożonym kształcie przekroju poprzecznego są od pewnego czasu przedmiotem żywego zainteresowania konstruktorów i projektantów ze względu na ich walory architektoniczne i użytkowe. Wyrazem tego były prace studialne i projekty wysokich kominów przemysłowych o przekrojach niepierścieniowych, opracowane przez Cieślika i in. [23, 25, 26,

109], Przykłady takich przekrojów, składających się z wycinków pierścieniowych, pokazano na rysunku 7.6. Określenie nośności rozpatrywanych przekrojów metodami analitycznymi nastręcza duże trudności natury obliczeniowej, dlatego też do ich wymiarowania lub sprawdzania wyko-rzystuje się najczęściej metodę elementów skończonych (MES), w której przekrój traktowany jest jak układ dyskretny. Analityczno-numeryczny sposób wyznaczania naprężeń w zakresie liniowo-sprężystym w mimo-środowo ściskanych przekrojach, przedstawionych na rysunku 7.6, zaproponowano w pracach [75, 105], Według tego podejścia uzyskano wykresy zależności współczynników B, C (por. rozdz. 5), określających największe naprężenia w betonie i w stali, w funkcji bezwymiarowego mi-mośrodu obciążenia e/R w odniesieniu do przekroju dwupierścieniowego (rys. 7.7, 7.8).

<)(>

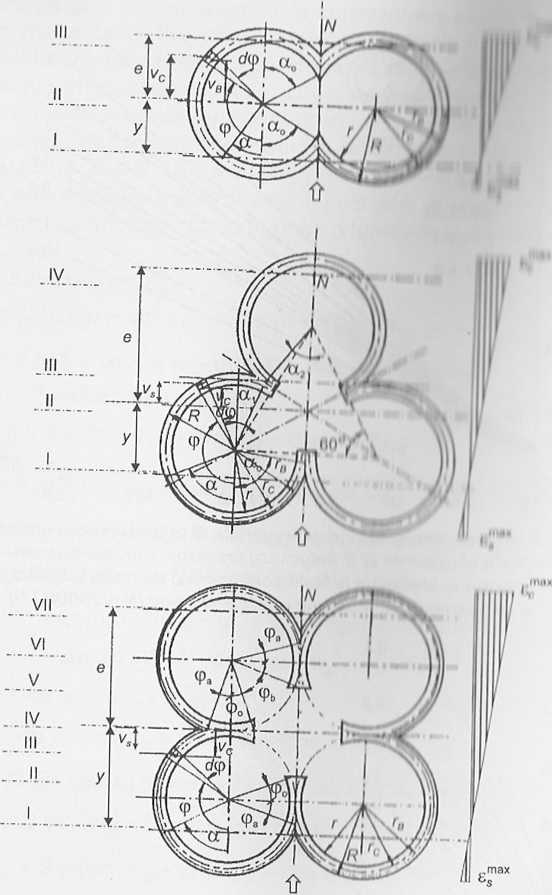
Rys- 7.6. Przykłady przekrojów złożonych z wycinków pierścieni

97