SIMPLEX przypadki szczególne rozwiązań

SZCZEGÓLNE PRZYPADKI ROZWIĄZAŃ

<0

c

N

U

CU

N

1_

o.

u)

OJ

c

ro

•a

ro

N

OJ

c

5

rei

c

i_

(U

d)

c

ro

E

a

o

«

< .2 3

N O

■ET

.zz

c

rei

0    —

n cu

u u

"E

ro

i_

01 O

<V

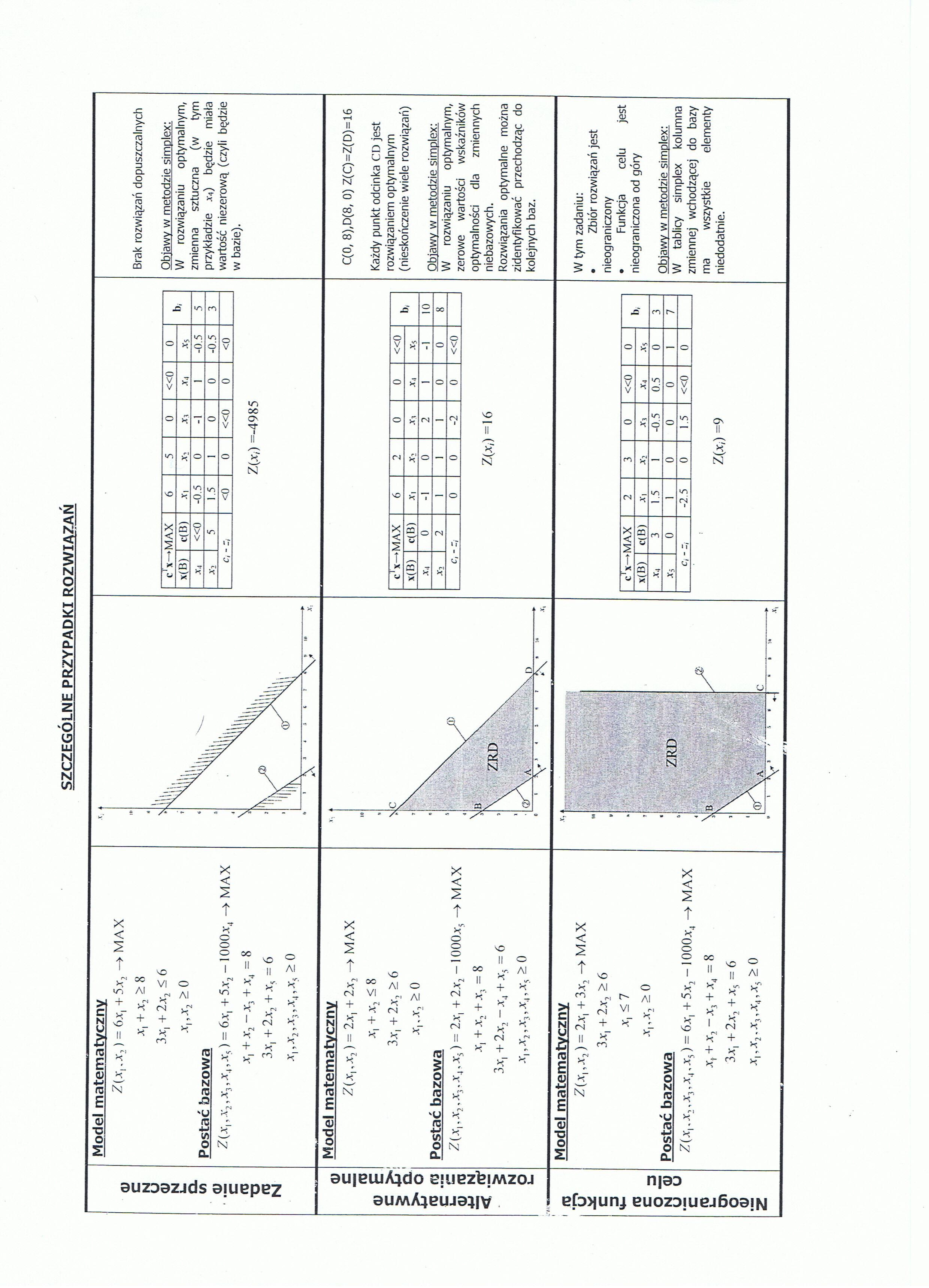
Model matematyczny

Z(x,.x₂) = 6x, + 5x, —» MAX x, + x₂ > 8 3x, + 2x₂ < 6 x,,x₂>0

Postać bazowa

Z(x,,x₂, x₃, x₄, x₅) = 6x, + 5x₂ -1000x₄ -> MAX x, + x₂ - x₃ + x₄ =8 3x, + 2x₂ + x, =6

X|,X₂,X₃,X₄,Xj > 0

Model matematyczny

Z(x,,Xj) = 2x, + 2x, —> MAX x, + x, < 8 3x, + 2x, > 6 x,.x, >0

Postać bazowa

Z(x,,x₂,x₃,x₄,x₅ ) = 2x, + 2x₂ - 1000x₅ —> MAX x, + x, + x, = 8 3x, + 2x, - x₄ + x, =6 Xj, x₂, x₃, x ,, x, >0

Model matematyczny

Z(x,,x₂) = 2x, +3x₂ —> MAX 3x, + 2x, > 6 x, < 7 x,,x₂ >0

Postać bazowa

Z(x_l.x₂,x₃,x₄,x₅) = 6x, + 5x, - 1000x₄ -X, + x₂ - x₃ + x₄ =8 3x, + 2x₂ + x₅ = 6 x,, x₂. x,, x₄, x₅ >0

MAX

c'x—>MAX		6	5	0	«0	0	b,
x(B)	c(B)	*1	Xz		*4	Xs
*4	«0	-0.5	0	-i	i	-0.5	5
X2	5	1.5	i	0	0	-0.5	3
C, - Z i		<0	0	«0	0	<0

Z(x/) =-4985

c'x->	MAX	6	2	0	0	«0
x(B)	c(B)	X\	X2	Xn	*4	x$
*4	0	-1	0	2	1	-i	10
X2	2	1	i	1	0	0	8
C,	Z i	0	0	-2	0	«0

Z(x,)=16

c'x—>MAX		2	3	0	«0	0	b,
*(B)	c(B)	A'|	Xi	Xi	*4	*5
x4	3	1.5	1	-0.5	0.5	0	3
*5	0	1	0	0	0	i	7
Ci - r,		-2.5	0	1.5	«0	0

Z(x,) =9

Brak rozwiązań dopuszczalnych

Obiawy w metodzie simplex:

W rozwiązaniu optymalnym, zmienna sztuczna (w tym przykładzie xą) będzie miała wartość niezerową (czyli będzie w bazie).

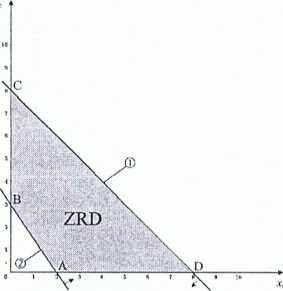
C(0, 8),D(8, 0) Z(C)=Z(D)=16

Każdy punkt odcinka CD jest rozwiązaniem optymalnym (nieskończenie wiele rozwiązań)

Obiawy w metodzie simplex:

W rozwiązaniu optymalnym, zerowe wartości wskaźników optymalności dla zmiennych niebazowych.

Rozwiązania optymalne można zidentyfikować przechodząc do kolejnych baz.

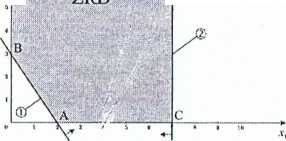
W tym zadaniu:

•    Zbiór rozwiązań jest nieograniczony

•    Funkcja celu jest nieograniczona od góry

Obiawy w metodzie simp|ex:

W tablicy simplex kolumna zmiennej wchodzącej do bazy ma wszystkie elementy niedodatnie.