wytrzTest002

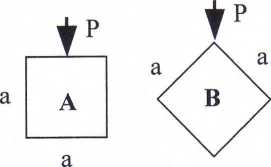
8. Ugięcia belek wspornikowych o długości L, obciążonych siłami skupionymi P przyłożonymi na końcach wsporników, o przekrojach ustawionych jak na rys. A i B są różne.

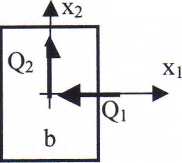
9. Rysunek przedstawia przekrój poprzeczny i działające w nim siły poprzeczne Qi i 6)2. Stosunek bezwzględnych wartości tych sił wynosi Qi/Q2=2. Stosunek maksymalnych naprężeń ^ stycznych 131/132 wynosi: - 2

10. Maksymalne naprężenie normalne c_x będzie 20 razy większe od maksymalnego naprężenia stycznego x dla stosunku L/h =100

A

L/2

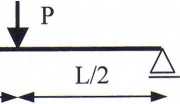
h

b

11. Nośność graniczna P* dla belki jak na rysunku wynosi 18 kN (Re = 200 MPa):

A

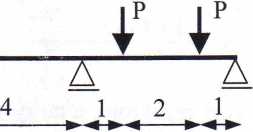
6

2

12.    O wytężeniu materiału w punkcie wg hipotezy Hubera-Misesa-Hencky’ego decyduje ikość nagromadzonej energii odkształcenia objętościowego

13.    Przy wyprowadzeniu równania linii ugięcia osi belki zginanej poprzecznie korzysta się z hipotezy płaskich przekrojów Bemouli’ego.

14.    Pręt o długości 2,0 m i polu przekroju 2 cm² rozciągany jest siłąP=500 kN. Wydłużenie pręta wynosi 2,5 cm, jeśli moduł Younga przyjęto E=200 GPa.

15.    Przypadek wytrzymałościowy, w którym obciążenie redukuje się w przekroju poprzecznym pręta do pary sił leżącej w płaszczyźnie prostopadłej do przekroju, ale nie będącej żadną z płaszczyzn głównych centralnych bezwładności to zginanie ukośne.

16.    Przekrój pręta ma kształt prostokąta o wymiarach b=2 cm i h=4 cm. Zwiększenie 3-krotne wymiaru „b” spowoduje 3-krotne zmniejszenie smukłości pręta

17.    Oś ciężkości i oś obojętna w przekroju belki wykonanej z materiału Prandtla i poddanej zginaniu prostemu w zakresie sprężysto-plastycznym nigdy się nie pokrywają.

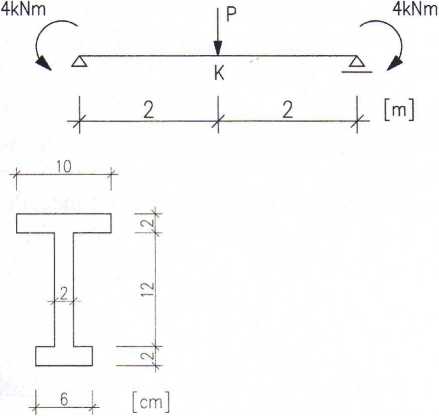
18. Ugięcie w punkcie K belki wynosi 2 cm, jeśli siła P ma wartość 15 kN (przyjąć EJ = 1000 kNm²)

19. Graniczny moment plastyczny dla podanego przekroju dwuteowego wynosi 144 kNm (przyjąć IU = 500 MPa).

20. Rdzeń przekroju to obszar geometryczny o tej własności, że jeżeli siła podłużna przyłożona jest w dowolnym jego punkcie to odpowiadająca jej oś obojętna leży poza przekrojem pręta lub jest do niego styczna.