002

yc y    oov^yk

y- rę-3,0 4-

dx ^

V

OJr-

<s( Lj-uowk -^ ^Y • CO) ol

^ _ dhi df

fd Yędf-) ok_

gjź ^v 51/1 °'^L

y cU - — k) y oo» OL

ivk Py* ~    foodd/oLO

i i <c ą    -    -    '

, 2 /J 'T'

IW

W

, M i ^    ~¥-^-_r-_i    '

/j y C<Jb L>4- f k) Y AĄ Ok,

' /J W

s\s&X> l O

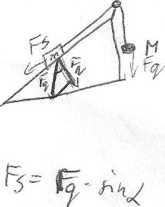
^ f

e*~

Ify^ĄAj-dk^ yjy '

<r= M'

h

~ !tz£j ~- A^- Ffy.ej-ihy

<\

fY

rr>

FjyzJk ~ A^/~'^ A<

~ —-

'    /-n

_ H/^r jVH~ ^

_- fy(*lftt k%t)

H

tf-t h

1/®^    /vix^

oj n» Cf ot £

^    dASC^OM

o-ajrę s

4V-?    /£E

f    f

[n~y    ^ i_s cixO t i/w?** y_

Y~ cr / o> fci+ &A ąs* £ .ce> ( y 6 + &J W^c P ■ ’ j?    oHcfy cy_cy    co> f^-p    £_J ^ y

ir- p '-*- ^ o

\    *    f, ,    °    /L    \

c] pvdy^<^ (f\yytixQYx-    i_r^OTl.—IP\

1 Ody OJ^cH ^ tliły mołHjY    ^ -

£_ 1 J p

W- o,t. f_t

o

(J / (j\dłt<d c    /v?^ ^v    ^ m

t    t

Pi: to-tĄy**,* ^ /to * o ł • --•^^-

P^: £i-l -

<^-⁴-*V^'-'

t*hW