335 (12)

670 26. Analiza obwodów nieliniowych

Przyjmujemy x — i, wobec tego dx

v = — = f_me “'(— x sin co ₀t + co ₀ cos co ₀t).

Jeżeli stała tłumienia jest mała, pominiemy dla uproszczenia wyraz asinco₀r; wprowadzając oznaczenie y = l_me ”, otrzymujemy

X = QSmC0₀t, - = QCOS(O₀t.

<-On

(26.48)

Równania te przedstawiają spiralę logarytmiczną. Trajektorią fazową w omawianym przypadku jest zatem spirala logarytmiczna owijająca się wokół początku układu współrzędnych (rys. 26.15).

Na tej podstawie wnioskujemy, że trajektoriom fazowym o postaci spirali owijających się wokół początku układu współrzędnych na płaszczyźnie fazowej odpowiadają drgania tłumione.

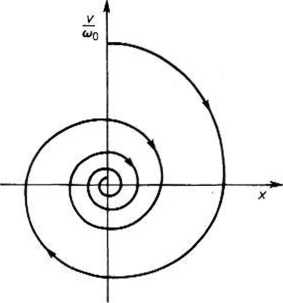
Rys. 26.15. Trajektoria fazowa w przypadku drgań tłumionych

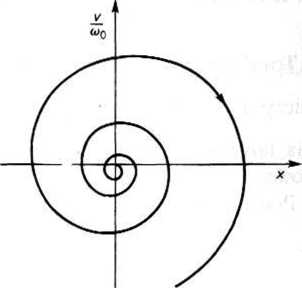
Rys. 26.16. Trajektoria fazowa w przypadku drgań rosnących

Gdy stała tłumienia a jest ujemna, wówczas wyrażenie (26.47) przedstawia drgania narastające, a trajektoria fazowa jest spiralą logarytmiczną odwijającą się (rys. 26.16). Wnioskujemy więc, że trajektoriom fazowym o postaci spirali od-wijających się odpowiadają drgania narastające.

Dla ol = 0 wyrażenie (26.47) przedstawia drgania nietłumione, a równania (26.48) przedstawiają okrąg: przypadek ten rozpatrywaliśmy w p. 26.8.1.

Przykłady trajektorii fazowych w przypadku przebiegów aperiodycznych tłumionych i narastających podane są na rys. 26.17.

Otrzymane wnioski mają charakter ogólny. Stwierdzamy, że na podstawie przebiegu trajektorii fazowych można otrzymać szereg informacji o zjawiskach występujących w badanych układach.

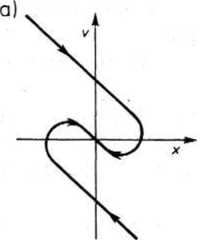
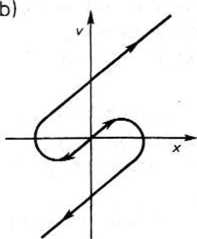
Rys. 26.17. Trajektorie fazowe w przypadku przebiegów aperiodycznych: a) przebiegi tłumione, b) przebiegi narastające

W prosty sposób można wyznaczyć zwrot, w którym punkt porusza się po trajektorii, czyli zwrot odpowiadający wzrostowi czasu. Przy dodatniej wartości v = dx/dt, czyli w górnej półpłaszczyźnie na płaszczyźnie fazowej, zmienna x rośnie, bowiem pochodna funkcji rosnącej jest dodatnia. Oznacza to, że w górnej półpłaszczyźnie ruch punktu musi odbywać się w kierunku wzrostu zmiennej x, czyli zgodnie ze zwrotem osi x. Łatwo sprawdzić, że w dolnej półpłaszczyźnie punkt przesuwa się przeciwnie do zwrotu osi x. Ogólnie można stwierdzić, że ruch punktu po trajektorii fazowej odbywa się w kierunku zgodnym z ruchem wskazówek zegara.

26.7.3. Cykl graniczny

W przypadku układów drgających, w których powstają okresowe drgania ustalone, trajektoria fazowa dąży do linii zamkniętej zwanej cyklem granicznym. Cykl graniczny odpowiada stanowi ustalonemu i obiegany jest jednokrotnie w ciągu okresu.

Trajektoria fazowa zaczyna się w punkcie płaszczyzny fazowej o współrzędnych dx

x₀ = x(0) oraz v₀ = — odpowiadającym warunkom początkowym i nawija się df _{( = 0}

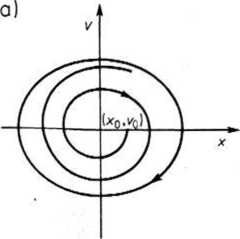
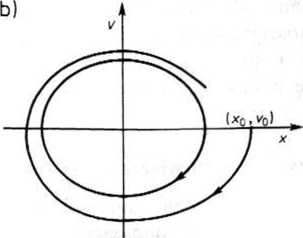
Rys. 26.18. Nawijanie się trajektorii fazowej na cykl graniczny: a) od wewnątrz, b) od zewnątrz