334 (15)

668 26. Analiza obwodów nieliniowych

26.7. Płaszczyzna fazowa

26.7.1. Określenia płaszczyzny fazowej i trajektorii fazowej

Płaszczyznę, w której na osi odciętych odkłada się wielkość x (np. napięcie, prąd itp.), a na osi rzędnych — pochodną v = dx/dt, nazywamy płaszczyzną fazową. Stan obwodu opisanego równaniem rzędu pierwszego lub drugiego charakteryzuje para wielkości x, r, czyli punkt o współrzędnych (x, u) na płaszczyźnie fazowej.

1 Wraz z upływem czasu, punkt (x, tj płaszczyzny fazowej przesuwa się wzdłuż linii nazywanej trajektorią fazową, a jej kształt zależy od postaci obwodu i od jego parametrów. Trajektoria fazowa w przypadku przebiegów okresowych jest krzywą zamkniętą, którą punkt {x, v) obiega jednokrotnie w ciągu okresu. Przy przebiegach nieokresowych, trajektoria fazowa jest krzywą niezamkniętą.

Dla obwodu opisanego równaniem różniczkowym pierwszego rzędu otrzymuje się jedną trajektorię, natomiast dla obwodu opisanego równaniem różniczkowym drugiego rzędu otrzymuje się rodzinę trajektorii fazowych. Na podstawie trajektorii fazowych można zbadać zjawiska występujące w obwodzie bez rozwiązywania równania różniczkowego.

Jako przykład rozpatrzymy równanie drgań harmonicznych

(26.43)

d²x ,

~Y + (ox = 0.

dr²

Wprowadzając oznaczenie

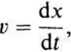
(26.44)

mamy

dr

d²x dr drdx

dt² d/ dx df ' ^ldx ’

wobec tego równanie (26.43) przybiera postać

(26.45)

dt' ₇

v—+co x - 0. dx

Po rozwiązaniu tego równania metodą rozdzielenia zmiennych, otrzymujemy

rdr = —cu²xdx,

a po scałkowaniu znajdujemy

v²    x²

— = — to²-— + const,

gdzie a jest stałą całkowania. Po przekształceniu otrzymujemy równanie elipsy

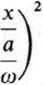
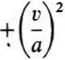
= 1.

(26.46)

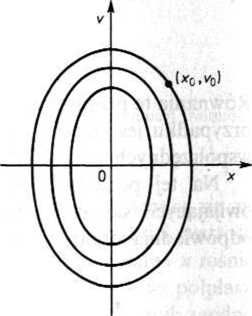
Rys. 26.14. Trajektorie fazowe równania różniczkowego (26.44)

Trajektorie fazowe równania (26.43) są elipsami (rys. 26.14). Stałą a można

; trajek

dx

d t

obliczyć na podstawie warunków początkowych x₀ = x(0) oraz v₀ =

torią fazową jest wówczas elipsa przechodząca przez punkt (x₀, v₀) płaszczyzny fazowej.

Podstawienie t = cot sprowadza równanie (26.43) do postaci

d²x

d?^+x-°-

Łatwo sprawdzić, że trajektoriami fazowymi tego równania są okręgi o środkach znajdujących się w początku układu współrzędnych.

26.7.2. Podstawowe własności trajektorii fazowych

Rozpatrzymy drgania w obwodzie o postaci połączenia szeregowego elementów R, L, C po włączeniu napięcia stałego E (p. 11.5.2). Prąd w tym połączeniu

i = /_me^_<”sincy₀f,    (26.47)

gdzie I_m = E/a>₀L, natomiast

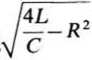
R    1

* ⁼ 2L’    ^a>0~ 2i

oznaczają stałą tłumienia oraz pulsację drgań własnych.