330 (14)

660 26. Analiza obwodów nieliniowych

r=0

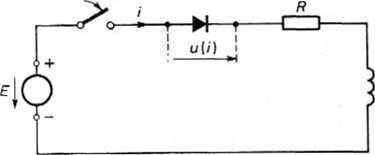
Rys. 26.8. Załączenie napięcia stałego do obwodu zawierającego prostownik i cewkę

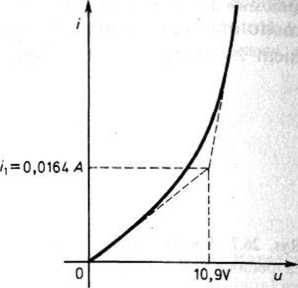
Rys. 26.9. Aproksymacja charakterystyki prostownika za pomocą linii łamanej

Dla pierwszego odcinka linii łamanej otrzymujemy równanie

di    i

10— + 500i +-= 40,    (26.16)

df    0,0015

czyli

di

— + 116,7i = 4. dr

Prąd ustalony

4

L =-= 0,0343 A,

116,7

a rozwiązaniem równania (26.16) przy zerowym warunku początkowym jest

i = 0,0343(1 -e“ⁿ⁶-⁷‘),    (26.17)

skąd znajdujemy, że prąd osiąga wartość i, =0,0164 A w chwili i_t = 0,00557 s. Wobec tego zależność (26.17) jest słuszna w przedziale 0 ^ r ^ 0,00557 s.

Dla drugiego odcinka otrzymuje się równanie

di    i+ 0,02

10— + 500i +-= 40,

dr    0,00333

czyli

— + 80i = 3,40.    (26.18)

dr

Prąd ustalony

3,40

i„ =-= 0,0425,

80

wobec tego rozwiązanie równania (26.18) przyjmujemy w postaci

i = 0,0425 + Ce-^8O<'-^,‘».    (26.19)

Stalą całkowania C znajdujemy z warunku, że i = 0,0164 A, gdy t = r, = 0,00557 s; otrzymujemy stąd

C = -0,0425 + 0,0164 = -0,0261,

wobec tego

i = 0,0425 — 0,0261 c ~ ⁸⁰⁽' ~¹¹ ’

dla r > i, — 0.00557 s.

26.4. Metoda aproksymacji analitycznej

Metoda polega na aproksymacji charakterystyki nieliniowej za pomocą funkcji, np. wielomianu, i podstawieniu tej funkcji do równania opisującego obwód; w ten sposób otrzymuje się nieliniowe równanie różniczkowe. W niektórych przypadkach otrzymane równanie daje się rozwiązać, a rozwiązanie ma wówczas postać zamkniętego wzoru, przedstawiającego poszukiwaną funkcję w zależności od czasu. Opisywana metoda jest metodą analityczną. Metodę tę przedstawiamy na przykładach.

Przykład 1. Wyznaczymy prąd w obwodzie zawierającym połączenie szeregowe opornika liniowego i cewki z rdzeniem stalowym (rys. 26.1) po włączeniu w chwili i =0 napięcia stałego.

Charakterystykę nieliniową cewki z rdzeniem stalowym aproksymujemy za pomocą wzoru

i = a>P²,    (26.20)

gdzie a jest wielkością stałą. Wzór (26.20) przedstawia tzw. aproksymacje paraboliczną.

Do równania napięciowego rozpatrywanego obwodu

(26.21)

(26.22)

dt/r

--(-/?/= E

dl

podstawiamy zależność (26.20), wobec tego otrzymujemy nieliniowe równanie

dil>

— + aRil/² = E.

dr

Równanie to rozwiązuje się metodą rozdzielenia zmiennych; mamy

di//

dr =-r,

E-aR\I/²

a stąd

*

t = i

o

d<j>

E-aR<!/²'

(26.23)

ze względu na zerowy warunek początkowy dla i!/.