337 (12)

674 26. Analiza obwodów nieliniowych

Z porównania wyrazów przy coscut oraz cos3a>t znajdujemy

(26.51)

— <u²/4₁ +a>oA₁ +4hAj + $hAiA₃+$hA_lAl = G, —9a)²A₃ + cooA₃ + łhAi + $hAlA₃ + $hA₃ = 0. Pierwsze równanie przedstawiamy w postaci

₂    , 3h _a2 G 3/j _j2[A₃ Ja₃\²'

W -®o+_T/(_i--+_Ta_l^—+2^-J .

Zakładając, że amplituda trzeciej harmonicznej jest bardzo mała w porównaniu z pierwszą harmoniczną, można pominąć iloraz A₃/A₁ w otrzymanym równaniu; wynika stąd równanie trzeciego stopnia

ihAl + ((Oo — o}²)A_l—G - 0,

z którego po rozwiązaniu otrzymuje się amplitudę A_t pierwszej harmonicznej.

Z drugiego równania znajdujemy wyrażenie

ihA]

^-9^-wt-łhAl-frAr

z którego po pominięciu wyrazu w mianowniku zawierającego A₃ oblicza się amplitudę A₃ trzeciej harmonicznej.

26.8.3. Zmiany skokowe amplitudy drgań

Rozpatrzymy nieliniowe równanie różniczkowe

d²x

dr²

(26.52)

dx

+ 2a—+ a>oX + hx³ = Gcosoit. dr

W szczególnym przypadku dla a = 0 otrzymuje się równanie Duffinga (26.49).

dx ,    .    ...

Ze względu na obecność wyrazu 2a—- w równaniu (26.52), pierwsza harmoniczna

dr

rozwiązania w stanie ustalonym jest przesunięta w fazie o kąt (p względem wymuszenia Gcos cot, a więc wyraża się wzorem 4cos(ft>t — <p). Istnienie tego przesunięcia w fazie można również uwzględnić, przyjmując funkcję wymuszającą w równaniu (26.52) w postaci Gcos(a»r+ <p), a pierwszą harmoniczną rozwiązania w postaci /łcoscor. W dalszych rozważaniach zastosujemy drugą możliwość, wobec tego zamiast równania (26.52) rozpatrzymy równanie

^-Ą + 2;x~ + u}ox + hx³ = Gcos (tur + <p),    (26.53)

dr dr

przy czym kąt cp zostanie wyznaczony w toku rozwiązania.

Do rozwiązania teeo równania różniczkowego zastosujemy metode bilansu

harmonicznych, przyjmując rozwiązanie w postaci x = /I cos cot. Mamy wówczas

— = —oj A sin cot, dr

d²x

dr²

—co²,4 cos cot,

x³ = /4³cos³a>r = ^>4³ (cos 3cot +3 cos cot), a po podstawieniu do równania (26.53), otrzymujemy

—oj² A cos cot — IclojA sin u>t + oj^A cos cot + \hA ³ (cos 3cot + 3 cos cot) =

= Gcostpcoscot — G sin <p sin oot.

Z porównania wyrazów zawierających cos co £ oraz sin cot wynikają równania

(coq — u>² + ihA²)A =Gcos(p,

2aco^l = Gsinę),

skąd znajdujemy

(26.54)

(26.55)

[(cog-co² + |/izl²)² + 4a²co²]^² = G², 2aco

^{tg(p =} oj²0-oj²+$h A²'

Rozwiązując równanie (26.54), znajdujemy amplitudę drgań, natomiast z zależności (26.55) oblicza się kąt przesunięcia fazowego tp.

Na podstawie równania (26.54) można wyznaczyć krzywą \A\ = /(co) dla danych wartości liczbowych co₀, a, h oraz G. Typowy wykres tej krzywej podano na rys. 26.21.

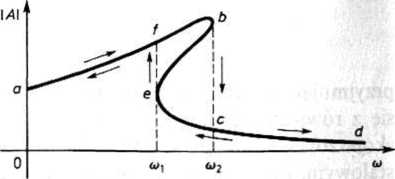
Rys. 26.20. Wykres amplitudy pierwszej harmonicznej rozwiązania równania różniczkowego (26.53) w funkcji pulsacji

Równanie (26.54) ma trzy pierwiastki rzeczywiste w przedziale co, < co < co₂, natomiast jeden pierwiastek rzeczywisty (i dwa zespolone) w przedziałach 0 < co < co, oraz co > co₂. Tłumaczy to kształt krzywej z rys. 26.20 dotyczącej rzeczywistych rozwiązań \A\ równania. W omawianym układzie występuje zjawisko zmiany skokowej amplitudy drgań przy zmianie pulsacji. Jeżeli pulsacja wzrasta od 0 do co₂, to amplituda \A\ zmienia się według łuku afb krzywej. Gdy co przekracza wartość co₂, wówczas występuje skokowe zmniejszenie się amplitudy od wartości