331 (12)

662 26. Analiza obwodów nieliniowych

Po obliczeniu całki w zależności (26.23) znajduje się

^t=^^arth (^/t)

gdzie y = ar thx jest odwrotną funkcją hiperboliczną, czyli x = thy. Otrzymane wyrażenie można

przedstawić w postaci

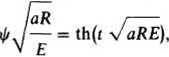
(26.24)

czyli strumień skojarzony cewki

(26.25)

(26.26)

I—th(r \JaRE). aR

Prąd w omawianym obwodzie wyznaczamy na podstawie zależności (26.20), wobec tego

(r s/aRE).

£

/ = -th² R

Przebiegi wielkości bezwymiarowych ip\/aR/E oraz iR/E przedstawione są na rys. 26.10 w zależności od wielkości t v aRE, która jest również bezwymiarowa. Przebieg prądu ma podobny charakter jak na

rys. 26.3.

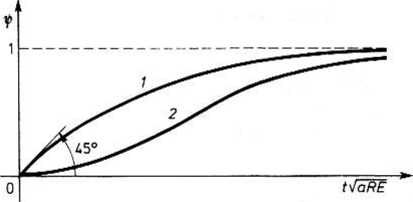
Rys. 26.10. Przebiegi strumienia skojarzonego i prądu w obwodzie z rys. 26.1: 1 — krzywa ip^/aR/E = th (t^/aRE),    2    — krzywa

iR/E = th²(f y/aRE)

Biorąc pod uwagę, że th x->l, gdy x->oc, znajdujemy na podstawie wzoru (26.26) prąd ustalony i„ = E/R, zgodnie z przewidywaniem.

Przykład 2. Rozwiążemy zagadnienie rozpatrywane w przykładzie 1 przy zastosowaniu innego rodzaju aproksymacji. Przyjmiemy mianowicie, że funkcję aproksymującą charakterystykę cewki z rdzeniem stalowym przedstawia wzór

i = a{e"*-l),    (26.27)

gdzie a, b są wielkościami stałymi. Zależność ta przedstawia tzw. aproksymację wykładniczą (por. p. 25.3.2). Podstawiając wyrażenie (26.27) do równania (26.21), otrzymujemy nieliniowe równanie

dtp

—+aR(e^b*-l) = E.    (26.28)

dr

Równanie to przekształcamy za pomocą podstawienia y = e^fc*, wobec tego

a stąd

di1/    1 dy

d(    by d(

Równanie (26.28) przybiera zatem postać

dy

—\-abR(y— l)v = F.by. dr

Równanie to rozwiązuje się metodą rozdzielenia zmiennych; mamy

dy

(26.29)

dr = —

a stąd

-J;

abR(y— 1 )y—bEy

d y

abR(y— 1 )y—bEy

Po obliczeniu całki znajdujemy

it = ln-

Ay

aRy — (E + aR)

gdzie A jest stalą całkowania, zaś i = h{E+aR)\ po przejściu do postaci wykładniczej, znajdujemy

(E + aR)c”

>’ =

a Re¹' — A

(26.30)

Stalą całkowania A wyznacza się z warunku, że dla t = 0 mamy i/r = 0, czyli y = e¹* = 1 i w wyniku znajdujemy A = — £; wobec tego po podzieleniu licznika i mianownika przez c" otrzymujemy

E+aR

aR + Ee ¹¹

Prąd w rozpatrywanym obwodzie wynosi

r = a(y-l) =

a£(l —e~“) aR + Ee * '

(26.31)

Gdy r-*x, otrzymujemy i-*E/R zgodnie z przewidywaniem.

Przykład 3. Kondensator w obwodzie z rys. 26.11 naładowany jest do napięcia U₀. Po zamknięciu wyłącznika, kondensator rozładowuje się przez opornik i prostownik. Wyznaczymy prąd płynący w omawianym obwodzie.

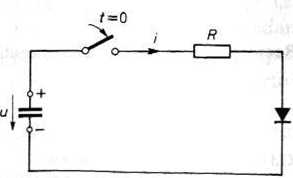
Rys. 26.11. Wyładowanie kondensatora przez opornik i prostownik