328 (18)

0

26. Analiza obwodów nieliniowych

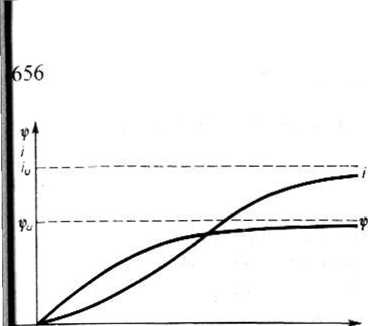
Rys. 26.3. Przebiegi strumienia skojarzonego i prądu w obwodzie z rys. 26.1 )mówionej w p. 25.1.2 przy wykorzystaniu nieliniowej charakterystyki elementu, snując przebieg strumienia skojarzonego. W wyniku otrzymuje się krzywą przed-itawioną na rys. 26.3. Wyznaczony w ten sposób przebieg prądu różni się znacznie )d krzywej

(26.8)

i = ijl -e "')

trzymanej na podstawie wzorów (26.4) i (26.7).

Omawiana metoda jest metodą graficzno-analityczną, bowiem pierwszy etap ma :harakter analityczny, a w drugim etapie znajduje się wynik na drodze graficznej, yletoda ta daje wyniki obarczone dużymi błędami i może nawet zniekształcić obraz :jawisk. gdy punkt A charakterystyki odpowiadający t = cc (rys. 26.2) znajduje się la jej części odpowiadającej dużym wartościom prądu i.

J6.2.3. Obwód zasilany napięciem sinusoidalnym

Do obwodu zawierającego cewkę z rdzeniem stalowym (rys. 26.4) włączone jest

C chwili r = 0 napięcie sinusoidalne u = l/_msin(cot + cp_u). Równanie napięciowe mawianego obwodu przybiera postać

-j~ + Ri = U_msin{(ot + (p_u).

dr

(26.9)

dokonując linearyzacji charakterystyki nieliniowej cewki, jak w p. 26.2.2, określamy ndukcyjność statyczną cewki za pomocą wzoru (26.3). Po podstawieniu prądu

t= o

R

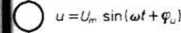
Rys. 26.4. Załączenie napięcia sinusoidalnego do połączenia szeregowego opornika i cewki z rdzeniem stalowym

z zależności (26.4) do równania (26.9), otrzymujemy

dtp 1 ,

- + -il/ = ^umsm((Dt + cp_u),    (26.10)

przy czym stałą czasową przedstawia wzór (26.6).

Ustalony strumień skojarzony wyraża się wzorem

tu = iA_msin ((ot + q>_u-q>),    (26.11)

gdzie

ę = arctg

R ’

(26.12)

bowiem w zlinearyzowanym obwodzie strumień skojarzony jest w fazie z prądem. Na podstawie zależności (26.3) znajdujemy

tm = LJm =

L_stU_m

JR² + co²LI'

(26.13)

bowiem _v R² +(O^zLj_l jest modułem impedancji zlinearyzowanego obwodu.

Przyjmujemy w dalszych rozważaniach, że rezystancja R jest bardzo mała w porównaniu z reaktancją cuL_s,; założenie to jest zwykle spełnione w rzeczywistych warunkach. Na podstawie wzorów (26.12) i (26.13) znajdujemy wówczas

(P

n

2’

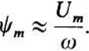
(26.14)

Zależności te określają wielkości ę oraz ip_m występujące we wzorze (26.11).

Rozwiązanie równania różniczkowego (26.10) przy zerowym warunku początkowym przybiera postać (por. p. 11.2.4) tp = ip_m[s\n(ajt + (p_u-(p)-e~"^lsm(<p_u-(pY\, a po podstawieniu <p = jt/2, mamy

iP = i/'_m[-cos(coH-<p_li) + e ^,/rcos<pJ.

Składowa przejściowa strumienia skojarzonego ma największą wartość początkową dla (p_u = 0; mamy wówczas

ip = ip_m(-cosa)t + e^_,/t).    (26.15)

Przebieg strumienia skojarzonego przedstawiony jest na rys. 26.5. Przebieg prądu w rozpatrywanym obwodzie wyznaczamy graficznie jak w p. 26.2.2 i w wyniku otrzymuje się krzywą przedstawioną na rys. 26.6.

Po włączeniu napięcia sinusoidalnego, prąd w cewce z rdzeniem stalowym może przybierać bardzo duże wartości, bowiem przy dostatecznie dużych wartościach strumienia skojarzonego odpowiednie punkty znajdują się na części spłaszczonej charakterystyki nieliniowej, gdzie niewielkim przyrostom strumienia ip odpowiadają