343 (11)

686 26. Analiza obwodów nieliniowych

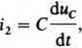
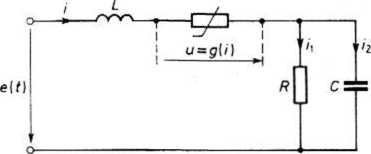
Po wyeliminowaniu prądu i, =i—u_c/R, otrzymujemy równania stanu:

di

dt

clu£_i dt ~ C CR

1 ^uc

Rys. 26.23. Przykład obwodu nieliniowego

Pierwsze równanie jest nieliniowe. Równania te przedstawiamy w postaci macierzowej

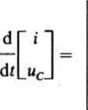
1 1 1

-e(f )—-»(*)—“^Mc

1 1

-i--u_c

C CR

Macierzowe równanie stanu dla obwodów nieliniowych można przedstawić w postaci ogólnej

^ = f(*(0, t),    (26.77)

gdzie f(x, f) jest funkcją macierzową o postaci macierzy kolumnowej. Całkując powyższe równanie, otrzymuje się nieliniowe równanie całkowe

r

x(t) = x(0) + Jf(x(T), r)dT,    (26.78)

o

Nie ma ogólnych metod rozwiązywania nieliniowych równań stanu, a rozwiązanie w postaci analitycznej można otrzymać tylko w bardzo nielicznych przypadkach. W tej sytuacji jedyną możliwością jest uzyskanie przybliżonego rozwiązania numerycznego, stosując metody numeryczne, na przykład omówione w p. 23.4: zmodyfikowaną metodę Eulera lub metodę Rungego-K-utty.

Bardzo ważnym zagadnieniem analizy układów nieliniowych jest badanie istnienia i jednoznaczności rozwiązania, gdyż wyznaczanie rozwiązania ma sens tylko wtedy, gdy rozwiązanie istnieje i jest jednoznaczne.

Przykładem równania nieliniowego pierwszego rzędu, nie mającego jednoznacz-

nego rozwiązania jest

2x>

dx

dr

z zerowym warunkiem początkowym x(0) = 0. Łatwo sprawdzić, że rozwiązanien tego równania jest

x(f) =

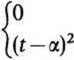
dla    0 < t ^ a,

dla    t > a,

gdzie a > 0 jest dowolną liczbą. Istotnie, spełnienie równania dla 0 < t < a ora: spełnienie warunku początkowego wynika natychmiast, natomiast dla t ^ a mam;

^ = 2(t-a) = 2[(r-a)²]* = 2xⁱ dt

dla dowolnego a > 0. Wynika stąd, że rozpatrywane równanie nie ma jednoznacz nego rozwiązania.

Obszerne informacje na temat analizy obwodów nieliniowych przy zastosowanii równań stanu są zawarte w pracach [5, 63].