327 (13)

654 26. Analiza obwodów nieliniowych

26.2. Metoda linearyzacji jednoodcinkowej

26.2.1. Uwagi ogólne

W metodzie linearyzacji jednoodcinkowej aproksymujemy charakterystykę nieliniową za pomocą linii prostej, wskutek czego zamiast równania różniczkowego nieliniowego otrzymuje się równanie liniowe. Metoda ta daje dobre wyniki, gdy charakterystyka nieliniowa odbiega nieznacznie od aproksymującej ją linii prostej, natomiast otrzymuje się wyniki mało dokładne, gdy charakterystyka nieliniowa znacznie odbiega od tej linii prostej. W niektórych przypadkach można poprawić dokładność przez zastosowanie w końcowym etapie rozwiązania metody graficznej wyznaczania przebiegu czasowego przy wykorzystaniu rzeczywistej charakterystyki nieliniowej.

Linię prostą aproksymującą charakterystykę nieliniową prowadzi się przez dwa punkty, a mianowicie przez punkty charakterystyki odpowiadające chwili początkowej i 0 oraz chwili / — x. w której występuje stan ustalony. Gdy charakterystyka nieliniowa jest symetryczna i przechodzi przez początek układu współrzędnych, wówczas chwili t = 0 przy zerowym warunku początkowym odpowiada początek układu współrzędnych. Prosta aproksymująca przechodzi więc w tym przypadku przez początek układu współrzędnych oraz przez punkt charakterystyki nieliniowej odpowiadający t = oc.

26.2.2. Obwód zasilany napięciem stałym

Na rysunku 26.1 przedstawiony jest obwód zawierający opornik liniowy o rezystancji R oraz cewkę z rdzeniem stalowym. W chwili t = 0 załączamy do obwodu

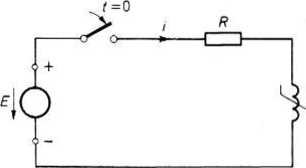
Rys. 26.1. Załączenie napięcia stałego do połączenia szeregowego opornika i cewki z rdzeniem stalowym

napięcie stałe E, a celem obliczeń jest prąd płynący w tym obwodzie. Równanie napięciowe dla badanego układu przedstawiamy w postaci

(26.1)

gdzie ip oznacza strumień skojarzony cewki; a warunek początkowy jest zerowy, czyli /(O) = 0.

W stanie ustalonym obwodu mamy dipjdt = 0, wobec tego prąd ustalony wynosi

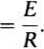
(26.2)

Prąd ustalony i_u wyznacza punkt charakterystyki nieliniowej ip(i) odpowiadający t = oo, a początek układu współrzędnych odpowiada chwili początkowej t = 0. Przyjmujemy, że prosta OA przechodząca przez te dwa punkty aproksymuje nieliniową charakterystykę, czyli jest tzw. zlinearyzowaną charakterystyką omawianego elementu nieliniowego (rys. 26.2).

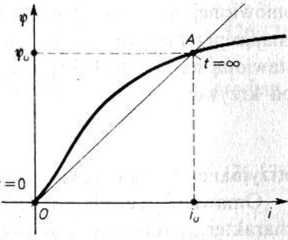
Rys. 26.2. Aproksymacja charakterystyki cewki nieliniowej za pomocą linii prostej

Indukcyjność statyczna cewki w punkcie A charakterystyki jest równa (por. p. 25.4.3)

Lu =    (26.3)

^lu

a w każdym punkcie zlinearyzowanej charakterystyki spełnione jest równanie

= LJ.    (26.4)

Podstawiając i z wzoru (26.4) do równania (26.1), otrzymujemy

dtp 1

■jr+-'!' = E,    (26.5)

df t

gdzie

T

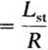
(26.6)

jest stałą czasową rozpatrywanego obwodu. Rozwiązaniem równania różniczkowego (26.5) przy warunku początkowym ip(0) = 0 jest

^ = ^(l-_e-'/‘).    (26.7)

Przebieg strumienia skojarzonego ip cewki podany jest na rys. 26.3.

Przebieg prądu w omawianym obwodzie znajdujemy za pomocą konstrukcji