332 (14)

664 26. Analiza obwodów nieliniowych

Charakterystykę połączenia szeregowego opornika i prostownika aproksymujcmy za pomocą wzoru

i — au + bu²,    u 0,    (26.32)

gdzie a, b są stałymi, zaś u jest napięciem na tym połączeniu szeregowym, które w tym przypadku równa się napięciu na kondensatorze.

Z jednej strony prąd w omawianym połączeniu wyraża się wzorem (26.32), a z drugiej strony

du

i = -C—; dr

znak minus pochodzi stąd, że na rys. 26.11 napięcie na kondensatorze ma zwrot przeciwny niż prąd. Wobec tego otrzymujemy

du

— C— = au + bu², dr

skąd wynika nieliniowe równanie różniczkowe

du

C— + au + fcu² =0,    (26.33)

dr

przy czym warunkiem początkowym jest u(0) = U₀. Równanie (26.33) rozwiązujemy metodą rozdzielenia zmiennych; mamy

Cdu

dr ---,

bu² + au

czyli

f du

r = -C -.

J bu² + au

Obliczamy całkę występującą w tym wyrażeniu i znajdujemy

Au    at

In----,

bu + a    C

gdzie A jest stałą całkowania; po przejściu do postaci wykładniczej otrzymujemy

Ac^u-b

(26.34)

gdzie a - a/C. Stałą całkowania A wyznaczamy na podstawie warunku początkowego u(0) = U₀ i otrzymujemy

a + bU₀

A =-.

U₀

Rozwiązaniem rozpatrywanego zagadnienia jest zatem wyrażenie

(26.35)

____aCo

(a + bil ₀)e*' — bil ₀

Gdy r-* oo, otrzymujemy u-*0.

26.5. Metoda całkowania graficznego

Metodę całkowania graficznego omówimy na przykładzie obwodu zawierająceg opornik i cewkę z rdzeniem stalowym, przy włączeniu w chwili f = 0 napięcia stałeg (rys. 26.1).

Równanie napięciowe rozpatrywanego obwodu:

(26.36

gdzie ip oznacza strumień skojarzony cewki, a stąd

df

dtp

E-Ri'

Całkując to wyrażenie przy założeniu, że i//(0) = 0, znajdujemy

*

o

di//

E-Ri'

(26S,

Funkcja podcałkowa l/(£ — Ri) zależy od strumienia i//, a jej wartości można obliczy na podstawie charakterystyki nieliniowej ip(i). Łatwo sprawdzić, że funkcja ta m asymptotę prostopadłą do osi i// w punkcie ip_u, odpowiadającym prądowi ustalone mu i_u = E/R. Typowy wykres funkcji podcałkowej z wzoru (26.37) podany jest n rys. 26.12.

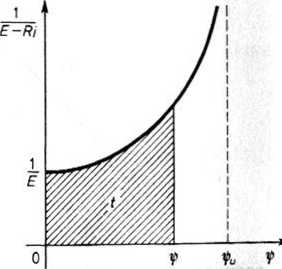
Rys. 26.12. Wykres funkcji podcałkowej ze wzoru (26.37) w zależności od strumienia skojarzonego cewki

Zgodnie z geometryczną interpretacją całki, całka we wzorze (26.37) przedstawi pole trapezu krzywoliniowego zakreskowanego na rys. 26.12, wobec tego cza f odpowiada (w pewnej skali) polu tego trapezu. Czas f odpowiadający zadam wartości strumienia ip wyznacza się, planimetrując pole wspomnianego trapezi W wyniku takiego postępowania otrzymujemy ciąg odpowiadających sobie wartośi t, ip, umożliwiających narysowanie krzywej tp(t).

Metoda całkowania graficznego jest bardzo prosta i znajduje częste zastosowa