333 (18)

666 26. Analiza obwodów nieliniowych

26.6 Metoda Preismana

Metoda Preismana służy do rozwiązywania graficznego nieliniowego równania różniczkowego pierwszego rzędu o postaci

dx

^a-^ + b^x+f(x) = c,    (26.38)

gdzie a, h, c są stałymi, a funkcja /(x) jest nieliniowa. Na wstępie omówimy sposób postępowania przy stosowaniu metody Preismana, a uzasadnienie podane będzie

później.

^f W układzie współrzędnych x, y rysujemy krzywą y =f(x) oraz prostą y = c — bx rys. 26.13). Punkt przecięcia się tych linii dotyczy stanu ustalonego; mamy bowiem wówczas dx/dt = 0, wobec tego z równania (26.38) znajdujemy

f(x) = c-bx,    (26.39)

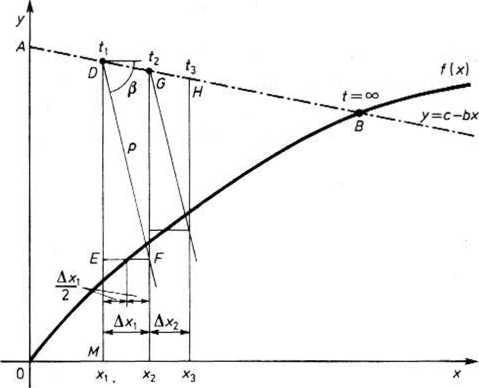
Rys. 26.13. Konstrukcja wykonywana przy stosowaniu metody Preismana

a rozwiązaniem tego równania jest punkt przecięcia obu rozpatrywanych linii. Punktom odcinka AB prostej y = c — bx odpowiadają określone wartości czasu t z przedziału (0, oo), a przy warunku początkowym x(0) = 0, punktowi A odpowiada czas t = 0.

Załóżmy, że punktowi D prostej y = c — bx odpowiada czas r,. Przyjmujemy stały odcinek czasowy Af i przez punkt D rysujemy prostą p tworzącą z osią x kąt fi obliczony z wzoru

(26.40)

ab

^{tg/J =} 4Ar

Następnie rysujemy odcinek EF równoległy do osi x w ten sposób, aby jego końce znajdowały się na rzędnej punktu D oraz na prostej p, a krzywa /(x) przechodziła przez środek tego odcinka. Długość wyznaczonego odcinka EF jest równa przyrostowi Ax, zmiennej x. Przez punkt F rysujemy równoległą do osi y i w przecięciu z prostą y = c — hx otrzymujemy punkt G. Odciętą punktu G jest x₂ = x,+dx_l, a odpowiada mu czas t, = t, + At.

Jeśli wykonamy opisaną konstrukcję w odniesieniu do punktu G, to znajdziemy punkt H o odciętej x, = x₂ + A.v,, któremu odpowiada czas t₃ = f₂ + Af. Powtarzając wielokrotnie tę konstrukcję otrzymamy kolejne wartości x_k oraz odpowiadające im czasy t_k, zbliżając się stopniowo do punktu B odpowiadającego stanowi ustalonemu. W rezultacie otrzymamy ciąg par wielkości t_k, x_k, które umożliwiają narysowanie przebiegu x(r).

Uzasadnienie opisanej konstrukcji jest następujące. Zastępując pochodną ilorazem różnicowym, przedstawiamy równanie (26.38) w postaci

Ax , ( Ax\ J Ax\

°^⁺T⁺t)^+/(^x+t)^=c'    ⁽²⁶-⁴¹¹

Ax .

przy czym x + -— jest wartością zmiennej x w środku przedziału Ax, ktorego

początek znajduje się w punkcie x. Po przekształceniu otrzymanego równania i po podstawieniu x = x,, otrzymujemy

⁺'i) ^Ax 1 = c ~¹ ~/(^X 1 +    •    (²⁶-⁴²)

Na podstawie rys. 26.13 znajdujemy

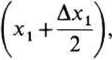
DM=c — bx₁    oraz EM =/

wobec tego

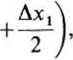
DE = DM-EM = c-bx_l-f(x₁

a z ADEF otrzymujemy

DE - EFtgfi = Ax, Igp.

Z porównania dwóch ostatnich zależności wynika spełnienie równania (26.42), jeśli spełnione jest równanie (26.40), co uzasadnia omawianą konstrukcję.

Metoda Preismana jest metodą graficzną, a rozwiązanie równania (26.38) uzyskuje się krok za krokiem. Wybór długości odcinka czasowego At jest wynikiem kompromisu, aby uzyskać dostateczną liczbę kroków obliczeniowych przy zachowaniu wystarczającej dokładności.