Nowe skanowanie 20080122080250 00000001A

16. Analiza obwodów prądu sinusoidalnego

Wówczas pozostałe napięcia zespolone

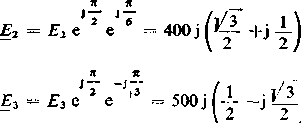
—200-|-j346,4

433+j250

Równania Kirchhoffa, stanowiące podstawę teorii obwodów elektrycznych, ze względu na znaczny nakład pracy konieczny przy posługiwaniu się nimi, są rzadko stosowane bezpośrednio do obliczania obwodów elektrycznych. W dążeniu do uproszczenia, usystematyzowania i większego zmechanizowania czynności wykonywanych przy obliczaniu obwodów elektrycznych, opracowano na podstawie równań Kirchhoffa kilka prostych metod obliczania obwodów, które wyprowadzono i omówiono szczegółowo w rozdziale 4, dotyczącym teorii obwodów prądu stałego.

Równania Kirchhoffa w obwodach prądów sinusoidalnych mają strukturę algebraiczną identyczną jak w obwodach prądu stałego z tą jedynie różnicą, że wszystkie napięcia, prądy i impedancje są wyrażone w postaci liczb zespolonych. Stąd wniosek, że wszystkie metody stosowane w teorii obwodów prądu stałego, a oparte na równaniach Kirchhoffa, mogą być stosowane do obwodów prądu sinusoidalnego przy użyciu metody liczb zespolonych. Można tu wymienić równania oczkowe, równania węzłowe, sposoby przekształcania obwodów, twierdzenie o wzajemności i in.

16.2. RÓWNANIA OCZKOWE

Równania oczkowe w sieciach prądów sinusoidalnych przybierają następującą postać ogólną:

Z11Z1+Z12/2+Z13I3+ ••• +Zl nLn ⁼    1

ZllLl +Z22 I2 +Z23 Z3 + ••• +Z2111n ⁼ LfE)2    (16.3)

Z.1 Zl + Z„2 I2 + Z„3 Z3 + • • • +Z„n La — (ZE)n

W równaniach (16.3) Z_mm oznacza impedancję własną m-tego oczka, równą sumie wszystkich impedancji rozmieszczonych wzdłuż konturu oczka m-tego, natomiast Zu oznacza impedancję wzajemną oczka k i oczka /. Impedancja wzajemna Z_ki jest równa impedancji gałęzi wspólnej dla oczek kil, opatrzonej znakiem (+), gdy prądy obu oczek w gałęzi wspólnej mają zwroty zgodne, a znakiem (—), gdy ich zwroty są przeciwne. Impedancja Z ki = 0, gdy oczka k i / nie mają gałęzi wspólnej. Impedancje własne Z_mra bierzemy zawsze ze znakiem (+), to znaczy, że wszystkie rezystancje mają wartości dodatnie, a reaktancje — znak wynikający z ich charakteru (indukcyjnego czy też pojemnościowego, gdyż X = X_L—X_C).

(S E)_m oznacza sumę wartości zespolonych napięć źródłowych w oczku w-tym. Napięcia źródłowe o zwrocie zgodnym z przyjętym zwrotem prądu Oczkowego opatrujemy znakiem (+), a napięcia o zwrocie przeciwnym — znakiem (—).

Liczba równań Oczkowych, analogicznie jak w sieciach prądu stałego (rozdz. 4), jest równa liczbie oczek niezależnych w danej sieci.

Stosowanie równań Oczkowych przedstawimy na konkretnym przykładzie.

Przykład 16.2. Wyznaczyć rozpływ prądów w obwodzie przedstawionym na rys. 16.1. Dane napięcia zasilające £j = 160+/160; E₂ — 190+j 100. Wartości rezystancji i reaktancji zaznaczono na rysunku.

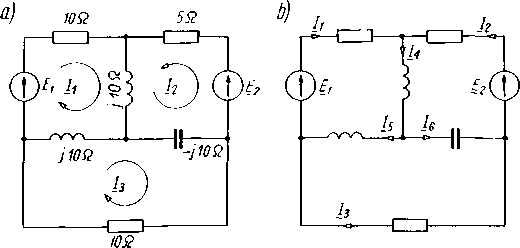
Rys. 16.1. Schemat obwodu do przykładu 16.2

Rozwiązanie. Zastosowawszy oznaczenia i zwroty prądów Oczkowych podane na rysunku i u-

względniwszy, że Z_u = 10+jl0+jl0 = 10+j20; Z₂₂ = 5+jl0—jlO = 5; Z₃₃ = 10+jI0— —jlO = 10, wypisujemy równania oczkowe

(10+j20)/₁+jl0/₂-jl0/₃ = 160+jl60    (16.4)

jlO/! + 5/₂ + (—jlO) /₃ = 190+jl00    (16.5)

—jl0/i + (—jlO) /2 + IO/3 = o    (16.6)

Podstawiając w równaniach (16.4) i (16.5) I₃ = j(|i+/₂) z równania (16.6) otrzymamy po obustronnym podzieleniu tych równań przez 10

(2+j2)/₁ + (l+j)/₂ = 16+jl6    (16.7)

(l+j)/i + l,5/₂ = 19+jl0    (16.8)

Mnożąc obie strony równania (16.8) przez 2 i odejmując stronami równanie (16.7) od równania (16.8) otrzymamy

(2—j)/₂ - 22+j4

skąd

1 = 22+j4 ₌ (22+j4) (2+j) = _{8 + j6} 2—j    5

Prąd h wyznaczamy z równania (16.8)

, 19+jlO —1,5/₂ _ 19+jlO —12—j9 _

1+j    1+j    ^J

485